
题目列表(包括答案和解析)
3. (86上海)
 Rt△ABC的两直角边长分别为AC=2,BC=3,P是斜边BC上一点,沿PC将起折为直二面角A-PC-B,此时AB=
Rt△ABC的两直角边长分别为AC=2,BC=3,P是斜边BC上一点,沿PC将起折为直二面角A-PC-B,此时AB= ,求二面角P-AC-B的大小
,求二面角P-AC-B的大小
2. (86(17)10分)如图,AB是圆O的直径,PA垂直于圆O所在的平面,C是圆周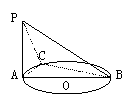 上不同于A,B的任意一点,求证:平面PAC⊥平面PBC.
上不同于A,B的任意一点,求证:平面PAC⊥平面PBC.
1. (85(13)15分) 如图,设平面AC和BD相交于BC,它们所成的一个二面角为45o,P为面AC内一点,Q为面BD内一点,圆周直线MQ是直线PQ在平面BD内的射影,并且M在BC中,又设PQ与平面BD所成的角为β,∠CMQ=θ(0o<θ<90o=,线段PM的长为a,求线段PQ的长.
如图,设平面AC和BD相交于BC,它们所成的一个二面角为45o,P为面AC内一点,Q为面BD内一点,圆周直线MQ是直线PQ在平面BD内的射影,并且M在BC中,又设PQ与平面BD所成的角为β,∠CMQ=θ(0o<θ<90o=,线段PM的长为a,求线段PQ的长.
6. (99(18)4分)α、β是两个不同的平面,m、n是平面α及β之外的两条不同直线,给出四个论断:①m⊥n,②α⊥β,③n⊥β,④m⊥α.以其中三个论断作为条件,余下一个作为结论,写出你认为正确的一个命题:_________________
5. (97(19)4分)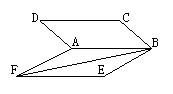 已知m,l是直线,α,β是平面,给出下列命题:
①若l垂直于α内的两条相交直线,则l⊥α;
②若l平行于α,则l平行于α内的所有直线;
③若m∩α,l∩β,且l⊥m,则α⊥β;
④若l∩β,且l⊥α,则α⊥β;
⑤若m∩α,l∩β,且α∥β,则m∥l.
其中正确的命题序号是____________(注:把你认为正确的命题的序号都填上)
已知m,l是直线,α,β是平面,给出下列命题:
①若l垂直于α内的两条相交直线,则l⊥α;
②若l平行于α,则l平行于α内的所有直线;
③若m∩α,l∩β,且l⊥m,则α⊥β;
④若l∩β,且l⊥α,则α⊥β;
⑤若m∩α,l∩β,且α∥β,则m∥l.
其中正确的命题序号是____________(注:把你认为正确的命题的序号都填上)
4. (96(19)4分)如图,正方形ABCD所在平面与正方形ABEF所在平面成60o的二面角,则异面直线AD与BF所成的角的余弦值为___________.
3. (93上海)正方体ABCD-A′B′C′D′中,过顶点B、D、C′作截面,则二面角B-DC′-C的大小为____________
2. (89(18)4分)如图,已知圆柱的底面半径是3,高是4,A,B两点分别在两底的圆周上,并且AB=5,那么直线AB与轴OO′之间的距离等于_________. 注:现行考试大纲指出:“对于异面直线的距离,只要求会计算已给出公垂线时的距离”。因此本题考察范围超出大纲要求。
1. (88(20)4分)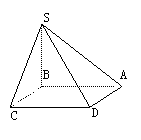
 如图,四棱锥S-ABCD的底面是边长为1的正方形,侧棱SB垂直于底面,并且SB=
如图,四棱锥S-ABCD的底面是边长为1的正方形,侧棱SB垂直于底面,并且SB= ,用α表示∠ASD,则sinα=__________.
,用α表示∠ASD,则sinα=__________.
30.(2001上海(15))若有平面 与
与 ,且
,且 ,则下列命题中的假命题为( )
,则下列命题中的假命题为( )
A.过点 且垂直于
且垂直于 的直线平行于
的直线平行于 . B.过点
. B.过点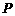 且垂直于
且垂直于 的平面垂直于
的平面垂直于 .
C.过点
.
C.过点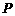 且垂直于
且垂直于 的直线在
的直线在 内. D.过点
内. D.过点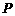 且垂直于
且垂直于 的直线在
的直线在 内.
内.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com