
题目列表(包括答案和解析)
8.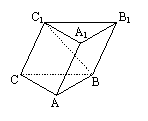 如图,在斜三棱柱A1B1C1-ABC中,∠BAC=900,BC1⊥AC,则C1在底面ABC上的射影H必在
如图,在斜三棱柱A1B1C1-ABC中,∠BAC=900,BC1⊥AC,则C1在底面ABC上的射影H必在
A、直线AB上 B、直线BC上
C、直线AC上 D、△ABC内部
7.平行六面体的棱长都为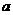 ,从一个顶点出发的三条棱两两都成600角,则该平行六面体的体积为
,从一个顶点出发的三条棱两两都成600角,则该平行六面体的体积为
A、 B、
B、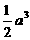 C、
C、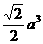 D、
D、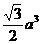
6.E,F分别是三棱柱ABC-A1B1C1的侧棱BB1和CC1上的点,且B1E=CF,则四棱锥A–BEFC的体积是原三棱柱体体积的
A、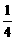 B、
B、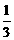 C、
C、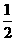 D、
D、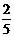
5.若斜线l与平面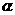 所成角为
所成角为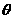 ,在
,在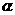 内任作l的异面直线
内任作l的异面直线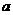 ,则l与
,则l与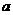 所成的角有
所成的角有
A、最大值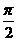 ,最小值
,最小值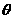 B、最大值
B、最大值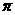 ,最小值
,最小值
C、最大值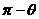 ,最小值
,最小值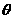 D、不存在最大值和最小值
D、不存在最大值和最小值
4.已知二面角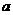 -l-
-l-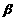 的大小为
的大小为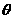 ,两异面直线
,两异面直线 、
、 ,
, ⊥
⊥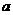 ,
, ⊥
⊥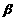 ,则
,则 、
、 所成角等于
所成角等于
A、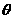 B、
B、 C、
C、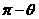 D、
D、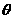 或
或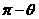
3.正四棱锥P-ABCD的侧面PAB为等边三角形,E是PC的中点,是异面直线BE与PA所成角的余弦值为
A、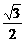 B、
B、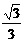 C、
C、 D、
D、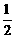
2.在棱长为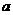 的正方体ABCD-A1B1C1D1中,与AD成异面直线,且距离为
的正方体ABCD-A1B1C1D1中,与AD成异面直线,且距离为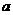 的棱共有
的棱共有
A、2条 B、3条 C、4条 D、5条
1.设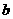 、
、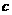 表示两条直线,
表示两条直线,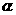 、
、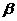 表示两个平面,下列命题中真命题是
表示两个平面,下列命题中真命题是
A、若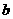
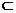
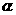 ,
,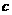 ∥
∥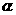 ,则
,则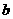 ∥
∥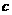 . B、若
. B、若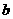
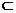
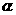 ,
,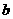 ∥
∥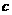 ,则
,则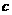 ∥
∥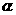 .
.
C、若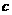 ∥
∥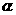 ,
,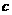 ⊥
⊥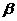 ,则
,则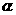 ⊥
⊥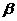 . D、若
. D、若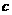 ∥
∥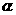 ,
,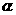 ⊥
⊥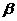 ,则
,则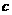 ⊥
⊥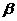 .
.
19(10分).求两条渐近线为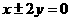 且截直线
且截直线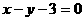 所得弦长为
所得弦长为 的双曲线方程。
的双曲线方程。
20(12分).已知空间三点 ,
,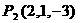 ,
,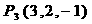 ,设
,设 ,
,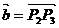
(1)求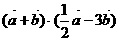 ;(2)求实数
;(2)求实数 ,使
,使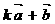 与
与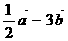 互相垂直.
互相垂直.
 21(12分).如图,正三棱柱ABC-A1B1C1中,AB=4,BB1=6, D为AB的中点,
F为A1C1中点,E在BB1上,
21(12分).如图,正三棱柱ABC-A1B1C1中,AB=4,BB1=6, D为AB的中点,
F为A1C1中点,E在BB1上,
(1)当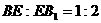 时,求异面直线CE与DF所成角的余弦
时,求异面直线CE与DF所成角的余弦
(2)在侧棱BB1上是否存在点P,使CP⊥DF,若存在,
求出BP的长;若不存在,请说明理由.
22(12分).函数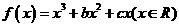 ,已知
,已知 是奇函数。
是奇函数。
(Ⅰ)求 、
、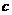 的值。
的值。
(Ⅱ)求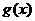 的单调区间与极值。
的单调区间与极值。
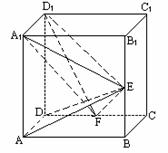 23(12分).如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点.
23(12分).如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点.
(Ⅰ)证明AD⊥D1F;(Ⅱ)求AE与D1F所成的角;(Ⅲ)证明面AED⊥面A1FD1;
24(12分).已知 在
在 与
与 时,都取得极值.
时,都取得极值.
(1) 求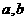 的值;(2)若
的值;(2)若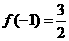 ,求
,求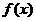 的单调区间和极值;
的单调区间和极值;
(3)若对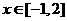 都有
都有 恒成立,求
恒成立,求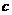 的取值范围.
的取值范围.
18.(1)已知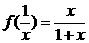 ,则
,则 _______.
_______.
(2)设函数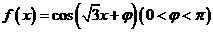 。若
。若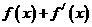 是奇函数,则
是奇函数,则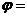 _______
_______
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com