
题目列表(包括答案和解析)
6.已知数列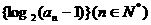 为等差数列,且
为等差数列,且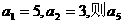 等于 ( )
等于 ( )
A.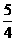 B.-3 C.1 D.5
B.-3 C.1 D.5
5.函数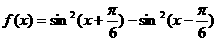 是 ( )
是 ( )
A.周期为π的奇函数 B.周期为π的偶函数
C.周期为2π的奇函数 D.周期为2π的偶函数
4.已知数列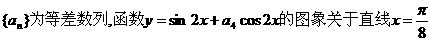 对称,则数列
对称,则数列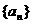 的前7项和S7等于 ( )
的前7项和S7等于 ( )
A.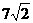 B.-
B.-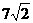 C.7 D.-7
C.7 D.-7
3.已知单位向量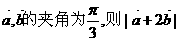 等于 ( )
等于 ( )
A.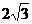 B.3 C.
B.3 C.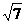 D.
D.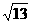
2.设全集为R,集合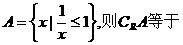 ( )
( )
A.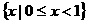 B.
B.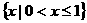
C.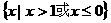 D.
D.
1.i虚数单位,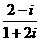 等于 ( )
等于 ( )
A.-i B.i C.-1 D.1
13.已知函数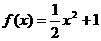 ,则过曲线
,则过曲线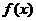 上的点(2,3)的切线方程为
上的点(2,3)的切线方程为
 14,若椭圆
14,若椭圆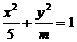 的离心率
的离心率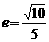 ,则
,则 的值是
的值是
15,已知一个与球心距离为2的平面截球所得的圆面面积为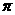 ,则
球的表面积是
,则
球的表面积是
 16,若过原点的直线L与曲线(x-2)2+y2=1有公共点,则直线的斜率的取值范围是
16,若过原点的直线L与曲线(x-2)2+y2=1有公共点,则直线的斜率的取值范围是

三,解答题:(本大题共6小题共70分。解答应写出文字说明,证明过程或演算步骤,请把答案写在答题纸的指定区域内)
17,(本小题满分12分)
已知双曲线的渐近线方程是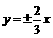 ,经过点
,经过点 ,求曲线的的标准方程。
,求曲线的的标准方程。
18, (本小题满分12分)
已知动圆过定点(1,0),且与直线x=-1相切,
(1)求动圆的圆心轨迹C的方程
(2)是否存在直线L,使L过点(0,1),并与轨迹C交于P、Q两点,且满足
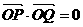 ?若存在,求出直线L的方程;若不存在,说明理由。
?若存在,求出直线L的方程;若不存在,说明理由。
19, (本小题满分12分)
如图所示,已知三棱锥P-ABC,∠ACB=90O,CB=4,AB=20,D为AB的中点,M为PB的中点,且△PDB是正三角形,PA⊥PC, P



 (1)求证:DM//平面PAC;
(1)求证:DM//平面PAC;


 (2)求证:平面PAC⊥平面ABC;
(2)求证:平面PAC⊥平面ABC;
(3)求三棱锥M-BCD的体积。 C M
A D B
20,(本小题满分12分)
椭圆的中心在原点,离心率e=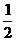 ,且它的一个焦点与抛物线y2=4x的焦点重合。
,且它的一个焦点与抛物线y2=4x的焦点重合。
(1) 求椭圆的方程;
(2) 设圆M经过椭圆的右顶点,且圆心M在抛物线y2=4x上,EG是圆M被y轴截得的弦,试探究当M运动,弦长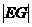 是否为定值?为什么?
是否为定值?为什么?
21,(本小题满分12分)
已知函数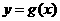 与
与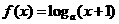 (
(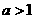 )的图象关于原点对称。
)的图象关于原点对称。
(1)写出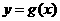 的解析式;
的解析式;
(2)若函数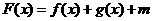 为奇函数,试确定实数
为奇函数,试确定实数 的值;
的值;
(3)当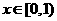 时,总有
时,总有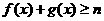 成立,求实数
成立,求实数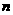 的取值范围。
的取值范围。
四,选做题:请考生在第22、23、24题中任选一题做答,如果多做,则按所做的第一题记分。
22, (本小题满分10分)(几何证明选讲)
已知AB是⊙O直径,ED切⊙O于D,EM⊥AB于M,交AD于C,交⊙O于F,
求证:EC=ED
23,(本小题满分10分)(坐标系与参数方程选讲)
已知直线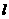 经过点
经过点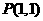 ,倾斜角
,倾斜角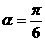 ,
,
(1)写出直线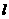 的参数方程。
的参数方程。
(2)设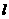 与圆
与圆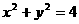 相交与两点
相交与两点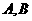 ,求点
,求点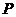 到
到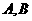 两点的距离之积。
两点的距离之积。
24,(本小题满分10分)(不等式选讲)
解不等式: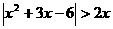
本资料由《七彩教育网》 提供!
16:(本小题满分12分)
已知 A、B 、C为ΔABC的三个内角,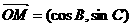 ,
, .
.
(Ⅰ)若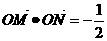 ,求角A大小;
,求角A大小;
(Ⅱ)若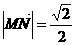 ,求
,求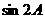 .
.
17:(本小题满分12分)
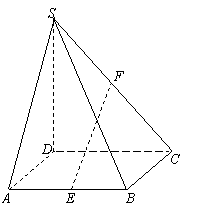 如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点.
如图,在四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E、F分别是AB、SC的中点.
(I) 求证:EF∥平面SAD;
(II) 设SD=2CD=2,求二面角A-EF-D的大小.
18:(本小题满分12分)
某高校自主招生程序分为两轮:第一轮:推荐材料审核;
第二轮分为笔试与面试。参加该校自主招生的学生只有通过第一轮推荐材料审核才有资格进入第二轮测试,否则被淘汰;在第二轮测试中若笔试与面试全部通过,则被确认为通过了自主招生考试;若仅通过了笔试而面试不通过,则被确认为通过自主招生的可能性为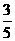 ;若仅通过面试而笔试不通过,则被确认为通过自主招生的可能性为
;若仅通过面试而笔试不通过,则被确认为通过自主招生的可能性为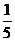 ;两者均不通过,则淘汰。现知有一报考该校自主招生的学生在推荐材料审核,笔试,面试这三环节中通过的概率分别为
;两者均不通过,则淘汰。现知有一报考该校自主招生的学生在推荐材料审核,笔试,面试这三环节中通过的概率分别为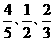 ,假设各环节之间互不影响.试求:
,假设各环节之间互不影响.试求:
(1)该生通过了第一轮及第二轮中的笔试却未通过该校自主招生的概率.
(2)该生未通过自主招生的概率.
19(本小题满分13分)
已知数列 中,
中,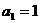 ,其前
,其前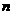 项和
项和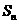 满足:
满足:
(1)
求 的通项
的通项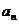 ;
;
(2)
令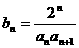 ,数列
,数列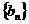 前项的和为
前项的和为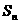 ,求证:
,求证: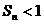
20:(本小题满分13分)
设函数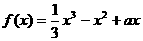 ,
,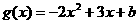 ,当
,当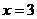 时,
时,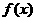 取得极值.
取得极值.
⑴求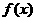 在
在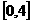 上的最大值与最小值.
上的最大值与最小值.
⑵试讨论方程: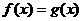 解的个数.
解的个数.
21:(本小题满分13分)
已知椭圆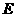 中心在坐标原点,焦点在坐标轴上,且经过
中心在坐标原点,焦点在坐标轴上,且经过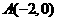 、
、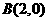 、
、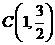 三点.
三点.
过椭圆的右焦点F任做一与坐标轴不平行的直线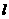 与椭圆
与椭圆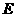 交于
交于 、
、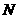 两点,
两点,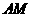 与
与 所在的直线交于点Q.
所在的直线交于点Q.
(1)求椭圆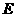 的方程:
的方程:
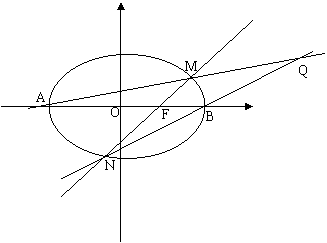 (2)是否存在这样直线
(2)是否存在这样直线 ,使得点Q恒在直线
,使得点Q恒在直线 上移动?若存在,求出直线
上移动?若存在,求出直线 方程,若不存在,请说明理由.
方程,若不存在,请说明理由.
9:方程为: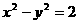 的双曲线离心率为:
的双曲线离心率为:
 10:为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为
10:为了调查某厂工人生产某种产品的能力,随机抽查了20位工人某天生产该产品的数量.产品数量的分组区间为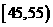 ,
,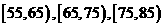 ,
, 由此得到频率分布直方图如下图,则这20名工人中一天生产该产品数量在
由此得到频率分布直方图如下图,则这20名工人中一天生产该产品数量在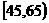 的人数大约是
的人数大约是
11:若两个向量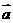 与
与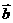 的夹角为,则称向量“
的夹角为,则称向量“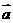

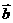 ”为“向量外积”,其长度
”为“向量外积”,其长度
|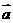

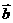 |=|
|=|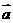 |•|
|•|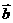 |•sin.
今已知|
|•sin.
今已知|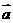 |=1,|
|=1,|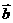 |=8,
|=8,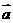 •
•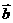 =-4,则|
=-4,则|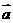

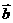 |=
|=
12:关于x的不等式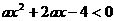 的解集为R,则实数
的解集为R,则实数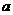 取值范围为
取值范围为
13:如果把个位数是4,且恰有3个数字相同的四位数叫做“吉祥数”,那么在由1,2,3,4四个数字组成的有重复数字的四位数中,“吉祥数”共有__ 个.
 14:若实数
14:若实数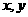 满足:
满足: 表示的区域的面积为
表示的区域的面积为
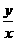 的取值范围是
的取值范围是
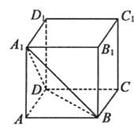
15:如图,正方体ABCD-A1B1C1D1棱长为1,则A到平面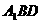 的距离为
,若P为线段
的距离为
,若P为线段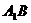 上一个动点,则
上一个动点,则 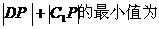
21.(本题满分13 分)
已知函数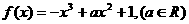
(1)若在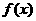 的图象上横坐标为
的图象上横坐标为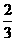 的点处存在垂直于y 轴的切线,求a 的值;
的点处存在垂直于y 轴的切线,求a 的值;
(2)若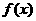 在区间(-2,3)内有两个不同的极值点,求a 取值范围;
在区间(-2,3)内有两个不同的极值点,求a 取值范围;
(3)在(1)的条件下,是否存在实数m,使得函数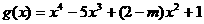 的
的
图象与函数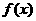 的图象恰有三个交点,若存在,试出实数m 的值;若不存在,说
的图象恰有三个交点,若存在,试出实数m 的值;若不存在,说
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com