
题目列表(包括答案和解析)
2.已知f(1)=3,f(n+1)=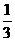 [3f(n)+1],n
[3f(n)+1],n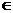 N*,则f(100)的值是
N*,则f(100)的值是
A.30 B.32 C.34 D.36
1.若集合M={y︱x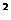 =y,x
=y,x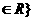 ,集合N={y︱x+y=0,x
,集合N={y︱x+y=0,x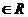 },则M
},则M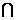 N等于
N等于
A.{y︱y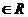 }
B.{(-1,1),(0,0)}
C.{(0,0)} D.{y︱y
}
B.{(-1,1),(0,0)}
C.{(0,0)} D.{y︱y 0}
0}
22.(本小题满分14分)
已知数列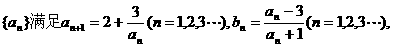
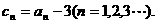
(I)若a1=2,证明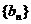 是等比数列;
是等比数列;
(II)在(I)的条件下,求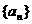 的通项公式;
的通项公式;
(III)若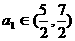 ,证明数列{|
,证明数列{| |}的前n项和Sn满足Sn<1.
|}的前n项和Sn满足Sn<1.
21、(本小题满分12分)
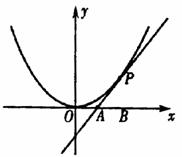 如图,已知直线
如图,已知直线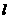 与抛物线
与抛物线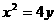 相切于点P(2,1),且与
相切于点P(2,1),且与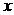 轴交于点
轴交于点 ,O为坐标原点,定点B的坐标为(2,0).
,O为坐标原点,定点B的坐标为(2,0).
(I)若动点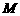 满足
满足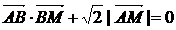 ,
,
求动点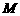 轨迹
轨迹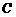 的方程;
的方程;
(II)若过点B的直线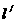 (斜率不等于零)与(I)
(斜率不等于零)与(I)
中的轨迹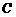 交于不同的两点E、F(E在B、F之间),
交于不同的两点E、F(E在B、F之间),
试求△OBE与△OBF面积之比的取值范围。
20、(本小题满分12分)
设 ,函数
,函数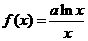 (1)讨论
(1)讨论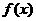 的单调性;
的单调性;
(2)求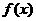 在区间
在区间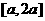 上的最小值。
上的最小值。
19、(本小题满分12分)
某公司欲建连成片的网球场数座,用128万元购买土地10000平方米,该球场每座的建筑面积为1000平方米,球场的总建筑面积的每平方米的平均建筑费用与球场数有关,当该球场建n个时,每平方米的平均建筑费用用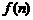 表示,且
表示,且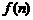
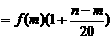 (其中
(其中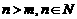 ),又知建五座球场时,每平方米的平均建筑费用为400元,为了使该球场每平方米的综合费用最省(综合费用是建筑费用与购地费用之和),公司应建几个球场?
),又知建五座球场时,每平方米的平均建筑费用为400元,为了使该球场每平方米的综合费用最省(综合费用是建筑费用与购地费用之和),公司应建几个球场?
18、(本小题满分12分)
正方体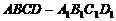 中,
中,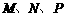 分别为棱
分别为棱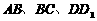 的中点.
的中点.
(1)求证: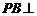 平面
平面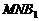 ;
;
(2)设二面角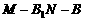 为
为 ,求
,求 的值。
的值。
17、(本小题满分12分)
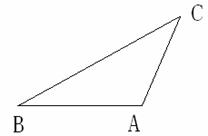 如图,在
如图,在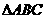 中,
中,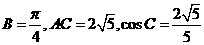 .
.
(Ⅰ)求 ;
;
(Ⅱ) 记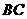 的中点为
的中点为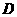 ,求中线
,求中线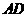 的长。
的长。

15.已知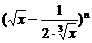 展开式中第4项为常数项,则展开式的各项的系数和为 .
展开式中第4项为常数项,则展开式的各项的系数和为 .
|
 =(-1,2)的直线(点法式)方程为
=(-1,2)的直线(点法式)方程为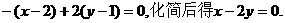 类比以上求法,在空间直角坐标系中,经过点A(2,1,3),且法向量为
类比以上求法,在空间直角坐标系中,经过点A(2,1,3),且法向量为 =(-1,2,1)的平面(点法式)方程为
.(请写出化简后的结果)
=(-1,2,1)的平面(点法式)方程为
.(请写出化简后的结果)14. 若体积为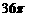 的球面上三点
的球面上三点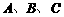 满足
满足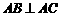 ,
,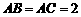 ,则球心到平面
,则球心到平面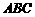 的距离为
.
的距离为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com