
题目列表(包括答案和解析)
6.设集合A={x|0≤x≤1},B={x|0≤x≤2},下面的对应中,是从A到B的函数的是( ).
A.f:x®3x B.f:x®x2 C.f:x®± D.f:x®2.5
5.下面的函数中是幂函数的是( ).
① y=x2+2; ②y=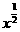 ; ③ y=2x3; ④y=
; ③ y=2x3; ④y=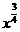 ; ⑤y=
; ⑤y=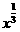 +1.
+1.
A.①⑤ B.①②③ C.②④ D.②③⑤
4.函数y=| x|-4的值域为 ( ).
A.(-∞,4] B.[-4,+∞) C.(-∞,-4] D.[4,+∞)
3.集合A={1,2}的真子集的个数是( ).
A.1 B.2 C.3 D.4
2.设集合A={x|-5≤x<3},B={x|x≤4},则A∪B=( ).
A.{x|-5≤x<3} B.{x|-5≤x≤4} C.{x|x≤4} D.{x|x<3}
1.方程组的解集是( ).
A.{x=0,y=1} B.{0,1} C.{(0,1)} D.{(1,0)}
21.(本小题满分13分)
已知函数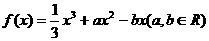 .
.
(I)若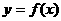 图象上的点(1,
图象上的点(1,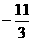 )处的切线斜率为一4,求
)处的切线斜率为一4,求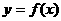 的极大值;
的极大值;
(Ⅱ)若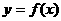 在区间
在区间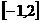 上是单调减函数,求a+b的最小值.
上是单调减函数,求a+b的最小值.
20.(本小题满分13分)
已知△OFQ的面积为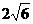 ,且
,且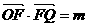 .
.
(I)设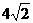 <m<
<m<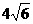 ,求向量
,求向量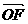 与
与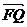 夹角
夹角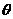 的取值范围;
的取值范围;
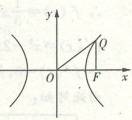
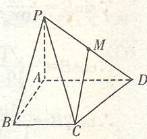
(Ⅱ)若以O为中心,F为焦点的双曲线经过点Q(如图),设F(c,0)
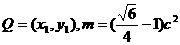 ,当︱
,当︱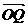 ︱取最小值时,求此双曲线的方程.
︱取最小值时,求此双曲线的方程.
18.(本小题满分12分)
甲,乙两人进行乒乓球比赛,在每一局比赛中,甲获胜的概率为P.
(I)如果甲,乙两人共比赛4局,甲恰好负2局的概率不大于其恰好胜3局的概率,试求P的取值范围.
(Ⅱ)若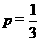 ,当采用3局2胜制的比赛规则时,求甲获胜的概率.-
,当采用3局2胜制的比赛规则时,求甲获胜的概率.-
(Ⅲ)如果甲,乙两人比赛6局,那么甲恰好胜3局的概率可能是 吗?为什么?
吗?为什么?

17.(本小题满分12分)
政府决定用“对社会贡献率”对企业进行评价,用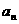 表示某企业第n年投入的治理污染费用,用
表示某企业第n年投入的治理污染费用,用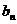 表示该企业第n年的产值.设
表示该企业第n年的产值.设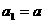 (万元),且以后治理污染费用每年都比上一年增加
(万元),且以后治理污染费用每年都比上一年增加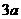 (万元);又设
(万元);又设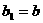 (万元),且企业的产值每年均比上一年增长10%,用
(万元),且企业的产值每年均比上一年增长10%,用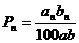 表示企业第n年“对社会贡献率”.
表示企业第n年“对社会贡献率”.
(I)求该企业第一年和第二年的“对社会贡献率”;
(Ⅱ)试问:从第几年起该企业“对社会贡献率”不低于30%?(参考数据:1.15=1.6105)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com