
题目列表(包括答案和解析)
3、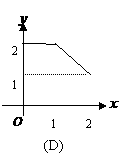

 设
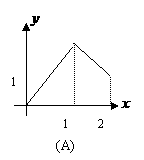
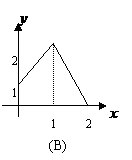
设 能表示从集合A到集合B的映射的是( )
能表示从集合A到集合B的映射的是( )
|
2、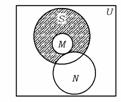 如图,U是全集,M,N,S是U的子集,则图中yin阴
如图,U是全集,M,N,S是U的子集,则图中yin阴
阴影部分所表示的集合是 ( )
A、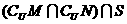 B、
B、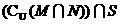
C、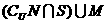 D、
D、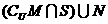
1、设集合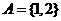 ,则满足
,则满足 的集合B的个数是 ( ) A、1
B、3 C、4 D、8
的集合B的个数是 ( ) A、1
B、3 C、4 D、8
17(本小题满分12分)已知 展开式的前三项系数成等差数列。
展开式的前三项系数成等差数列。
(1)
求这个展开式的 ;
;
(2) 求这个展开式的一次项。
18. (本小题满分12分) 如图,已知长方体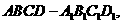
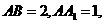
 直线
直线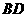 与平面
与平面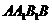 所成的角为
所成的角为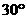 ,
,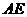 垂直
垂直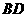 于
于
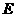 ,
,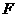 为
为 的中点.
的中点.
(1)求异面直线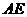 与
与 所成的角;
所成的角;
(2)求平面 与平面
与平面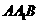 所成的二面角;
所成的二面角;
(3)求点 到平面
到平面 的距离.
的距离.
19(本小题满分12分)某单位组织4个部门的职工旅游,规定每个部门只能在峨眉山、泰山、华山3个景区中任选一个,假设各部门选择每个景区是等可能的.
(Ⅰ)求3个景区都有部门选择的概率;
(Ⅱ)求恰有2个景区有部门选择的概率.
20(本小题满分12分)已知等差数列的前三项为a,4,3a,前n项和为Sn ,若前k项和为Sk=2550
(1)求k的值;
(2)求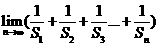 的值
的值
21(本小题满分12分)在一次篮球练习课中,规定每人投篮5次,若投中2次就称为“通过”若投中3次就称为“优秀”并停止投篮。已知甲每次投篮投中概率是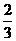 。
。
(1) 求甲恰好投篮3次就“通过”的概率;
(2)
设甲投中篮的次数为 ,求随机变量
,求随机变量 的分布列及期望
的分布列及期望 。
。
22(本小题满分12分)如图直棱柱ABC-A1B1C1中AB= ,AC=3,BC=
,AC=3,BC=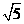 ,D是A1C的中点E是侧棱BB1上的一动点。
,D是A1C的中点E是侧棱BB1上的一动点。
(1) 当E是BB1的中点时证明:DE//平面A1B1C1;
(2)
求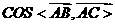 的值
的值
(3)
在棱 BB1上是否存在点E,使二面角E-A1C-C是直二面角?若存在求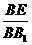 的值,不存在则说明理由。
的值,不存在则说明理由。
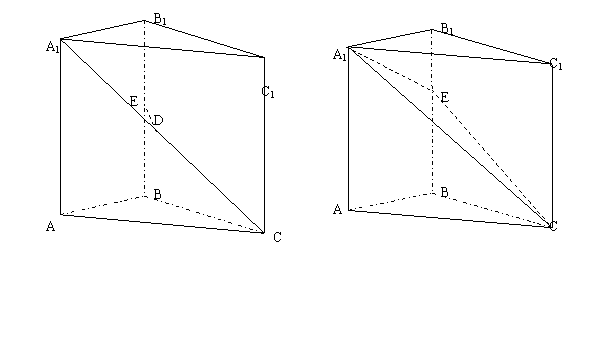

(13) ;(14) ;
(15) ;(16) ;
(13) 设等比数列{an}(n∈N)的公比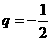 ,且
,且 ,则a1= ;
,则a1= ;
(14) 已知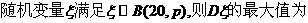 ;
;
(15)从0,1,2,3,5,7,11中任取3个元素分别作为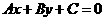 中的
中的 ,所得恰好经过原点的直线的概率为
;
,所得恰好经过原点的直线的概率为
;
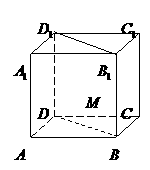
 (16)
正方体
(16)
正方体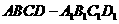 中棱长为
中棱长为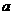 ,点
,点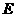 为
为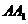 的中点,在对角面
的中点,在对角面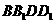 上取一点
上取一点 ,使
,使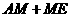 最小,其最小值为
。
最小,其最小值为
。
|
(理科)
 第Ⅱ卷(命题学校 成都八中)
第Ⅱ卷(命题学校 成都八中)
(1) 从2008个学生中选取100人志愿者,若采用下面的方法选取,先用简单随机抽样法从2008人中剔除8人,剩下的2000人按年级分层抽样取出100人,则每人入选的概率为( )
(A)不全相等
(B)均不相等 (C) (D)
(D)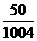
(2) 在正四面体P-ABC,已知M为AB的中点,则PA与CM所成角的余弦值为( )
(A) (B)
(B)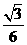 (C)
(C) 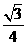 (D)
(D)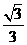
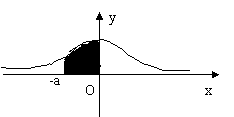 (3) 下图是正态分布N(0,1)的正态分布曲线图,下面4个式子中,能表示图中阴影部分面积的有(
)个
(3) 下图是正态分布N(0,1)的正态分布曲线图,下面4个式子中,能表示图中阴影部分面积的有(
)个
①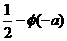 ②
②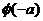
③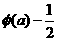 ④
④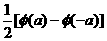
(A)1 (B)2 (C)3 (D)4
(4) (4) 设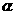 、
、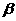 为两个不同的平面,
为两个不同的平面, 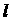 、
、 为两条不同的直线,且
为两条不同的直线,且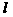
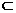
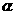 ,
, 
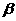 ,有如下的两个命题:①若
,有如下的两个命题:①若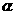 ∥
∥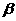 ,则
,则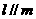 ;②若
;②若 ⊥
⊥ ,则
,则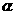 ⊥
⊥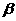 .那么( )
.那么( )
(A) ①是真命题,②是假命题 (B) ①是假命题,②是真命题
(C) ①②都是真命题 (D) ①②都是假命题
(5) 五个工程队承建某项工程的五个不同的子项目,每个工程队承建1项,其中甲工程队不能承建1号子项目,则不同的承建方案共有( )
(A)4种 (B)96种 (C)1种 (D)24种
(6) 设 ,
,
则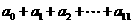 的值为( )
的值为( )
A.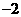 B.
B.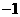 C.
C.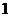 D.
D.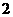
(7) 设地球的半径为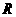 ,若甲地位于北纬
,若甲地位于北纬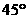 东经
东经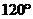 ,乙地位于南纬
,乙地位于南纬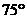 东经
东经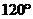 ,则甲、乙两地的球面距离为 ( )
,则甲、乙两地的球面距离为 ( )
(A)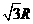 (B)
(B)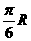 (C)
(C) (D)
(D)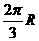

(8) 三条射线OA、OB、OC两两成角600则直线OA与平面OBC的成角为( )
(A)600 (B)450 (C) (D)
(D) 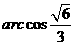
(9)北京奥运会期间,某高校有14名志愿者参加服务工作.若每天排早、中、晚三班,每班4人,每人每天最多值一班,则开幕式当天不同的排班种数为 ( )
(A)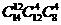 (B)
(B)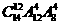 (C)
(C)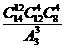 (D)
(D)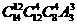
(10) 已知正方形ABCD折成直二面角A-BD-C则二面角B -CD-A的大小为( )
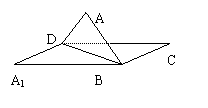
(A)600 (B)450
(C) 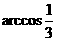 (D)
(D) 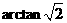
(11)5颗骰子同时掷出,共掷100次则至少一次出现全为6点的概率为( )
(A) 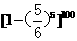 (B)
(B) 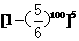 (C)
(C) 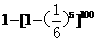 (D)
(D) 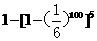
(12)已知直线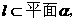 经过
经过 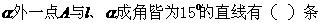
(A) 1 (B) 2 (C) 3 (D) 4
21.( 14分)
已知 是定义在[-1,1]上的奇函数,且
是定义在[-1,1]上的奇函数,且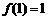 ,若
,若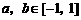 ,
,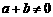 时,有
时,有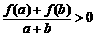 .
.
(1)判断函数 在[-1,1]上是增函数,还是减函数,并证明你的结论;
在[-1,1]上是增函数,还是减函数,并证明你的结论;
(2)解不等式: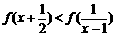 ;
;
(3)若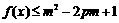 对所有
对所有 ,
, (p是常数)恒成立,求实数m的取值范围.
(p是常数)恒成立,求实数m的取值范围.
20.(
13分)已知二次函数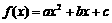 和一次函数
和一次函数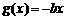 ,其中实数a、b、c满足
,其中实数a、b、c满足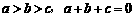 .
.
(1)求证:两函数的图象交于不同的两点A、B;
(2)求线段AB在x轴上的射影A1B1的长的取值范围.
19.(
12分) 函数 对一切实数x,y均有
对一切实数x,y均有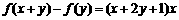 成立,且
成立,且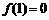 .
.
(1)求 的值;
的值;
(2)当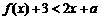 在
在 上恒成立时,求a的取值范围.
上恒成立时,求a的取值范围.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com