
题目列表(包括答案和解析)
1.若全集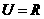 ,集合
,集合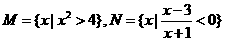 ,则
,则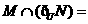 (
)
(
)
A. B.
B.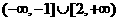 C.
C.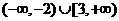 D.
D.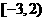
22.(本小题满分14分)已知函数 为实数),
为实数),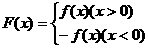
(1)若f(-1) = 0且对任意实数均有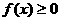 成立,求
成立,求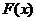 表达式;
表达式;
(2)在(1)的条件下,当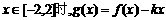 是单调函数,求实数k的取值范围;
是单调函数,求实数k的取值范围;
(3)(理科学生做)设 为偶函数,判断
为偶函数,判断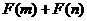 能否大于0.
能否大于0.
高三 数学 试卷
(请在相应选项上打“√”:文科□ 理科□)
(考试时间:120分钟;满分150分)
20.(本小题满分12分) 为了响应国家开发西部的号召,沿海地区A公司决定一次性投次156万元,从下个月开始对西部地区B企业进行扶持性技术改造.B企业的经营现状是:①每月收入为45万元;②因设备老化,从下个月开始需支付设备维修费,第一个月为3万元,以后逐月递增2万元.据预测,经更新设备等技术改造后,B企业第一个月的收入应为16万元,在以后的3个月中,每月的收入都将比上个月增长50%,而后各月的收入都会稳定在第4个月的水平上,假设改造时间和其它费用忽略不计.
(Ⅰ)如果B企业按现状一直生产下去,从下个月开始,最多可维持多少个月使得其每月的收入不少于当月需要支付的设备维修费?
(Ⅱ)从下个月开始至少经过多少个月,改造后的B企业的累计净收入不少于仍按现状生产所带来的累计净收入?(注:净收入=收入-投资或设备维修费.)
21(文科学生做)(本小题满分12分)
已知数列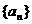 ,设Sn是数列的前n项和,并且满足a1=1,对任意正整数n,
,设Sn是数列的前n项和,并且满足a1=1,对任意正整数n,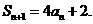
(1)令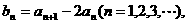 证明
证明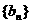 是等比数列,并求
是等比数列,并求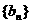 的通项公式;
的通项公式;
(2)令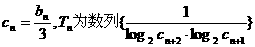 的前n项和,求
的前n项和,求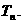
21 (理科学生做)(本小题满分12分)
已知数列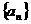 中,
中,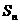 是其前
是其前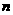 项和,并且
项和,并且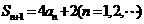 ,
,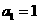

⑴设数列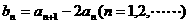 ,求证:数列
,求证:数列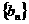 是等比数列,并求
是等比数列,并求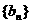 的通项公式;
的通项公式;
⑵设数列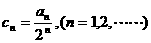 ,求证:数列
,求证:数列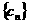 是等差数列,并求
是等差数列,并求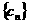 的通项公式;
的通项公式;
⑶求数列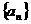 的通项公式及前
的通项公式及前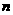 项和
项和
19.(本小题满分12分)设函数
(1)写出函数f(x)的最小正周期及单调递增区间;
(2)若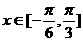 时,函数f(x)的最小值为2,求此时f(x)的最大值,并指出x为何值时,f(x)取得最大值.
时,函数f(x)的最小值为2,求此时f(x)的最大值,并指出x为何值时,f(x)取得最大值.
18.(本小题满分12分)
已知A、B、C的坐标分别为A(3,0),B(0,3),C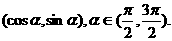
(I)若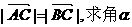 的值; (Ⅱ)若
的值; (Ⅱ)若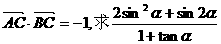 的值.
的值.
17.(本小题满分12分)已知圆C和y轴相切,圆心C在直线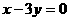 上,且被直线y=x截得的弦长为
上,且被直线y=x截得的弦长为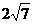 ,求圆C的方程.
,求圆C的方程.
16.如图,平面中两条直线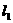 和
和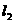 相交于点O,对于平面上任意一点M,若
相交于点O,对于平面上任意一点M,若 、
、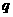 分别是M到
分别是M到
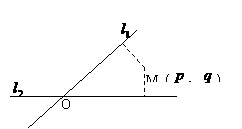 直线
直线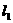 和
和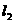 的距离,则称有序非负实数对(
的距离,则称有序非负实数对( ,
,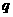 )是点M的“距离坐标”.
)是点M的“距离坐标”.
已知常数 ≥0,
≥0,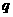 ≥0,给出下列命题:
≥0,给出下列命题:
① 若 =
=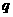 =0,则“距离坐标”为(0,0)的
=0,则“距离坐标”为(0,0)的
点有且仅有1个;
② 若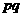 =0,且
=0,且 +
+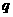 ≠0,则“距离坐标”为
≠0,则“距离坐标”为
( ,
,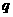 )的点有且仅有2个;
)的点有且仅有2个;
③ 若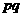 ≠0,则“距离坐标”为(
≠0,则“距离坐标”为( ,
,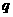 )的点有且仅有4个.
)的点有且仅有4个.
上述命题中,正确的命题有 (填写序号)
15.等差数列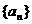 的第3、7、10项成等比数列,那么这个等比数列的公比q=
的第3、7、10项成等比数列,那么这个等比数列的公比q=
14、已知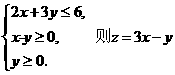 的最大值为 。
的最大值为 。
13、已知函数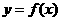 为奇函数,若
为奇函数,若 ,则
,则 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com