
题目列表(包括答案和解析)
21.(14分)椭圆G: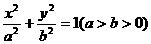 的两个焦点为F1、F2,短轴两端点B1、B2,已知F1、F2、B1、B2四点共圆,且点N(0,3)到椭圆上的点最远距离为
的两个焦点为F1、F2,短轴两端点B1、B2,已知F1、F2、B1、B2四点共圆,且点N(0,3)到椭圆上的点最远距离为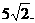
(1)求此时椭圆G的方程;
(2)设斜率为k(k≠0)的直线m与椭圆G相交于不同的两点E、F,Q为EF的中点,问E、F两点能否关于过点P(0,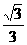 )、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.
)、Q的直线对称?若能,求出k的取值范围;若不能,请说明理由.
20.(14分)已知数列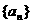 的前n项和为
的前n项和为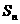 ,且满足
,且满足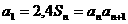
(1)求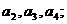
(2)求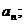
(3)若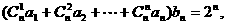 求证:
求证: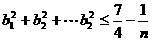 .
.
19.(14分)已知函数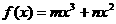 (m、n∈R,m≠0)的图像在(2,
(m、n∈R,m≠0)的图像在(2,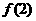 )处的切线与x轴平行.
)处的切线与x轴平行.
(1)求n,m的关系式并求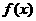 的单调减区间;
的单调减区间;
(2)证明:对任意实数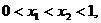 关于x的方程:
关于x的方程:
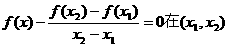 恒有实数解.
恒有实数解.
(3)结合(2)的结论,其实我们有拉格朗日中值定理:若函数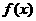 是在闭区间[a,b]上连续不断的函数,且在区间(a,b)内导数都存在,则在(a,b)内至少存在一点x0,使得
是在闭区间[a,b]上连续不断的函数,且在区间(a,b)内导数都存在,则在(a,b)内至少存在一点x0,使得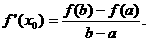 如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明:
如我们所学过的指、对数函数,正、余弦函数等都符合拉格朗日中值定理条件.试用拉格朗日中值定理证明:
当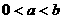 时,
时,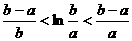 (可不用证明函数的连续性和可导性)
(可不用证明函数的连续性和可导性)
18.(14分)如图,已知几何体ABC-DEF中,△ABC及△DEF都是边长为2的等边三角形,四边形ABEF为矩形,且CD=AF+2,CD∥AF,O为AB中点.
(1)求证:AB⊥平面DCO.
(2)若M为CD中点,AF=x,则当x取何值时,使AM与平面ABEF所成角为45°?试求相应的x值.
 (3)求该几何体在(2)的条件下的体积.
(3)求该几何体在(2)的条件下的体积.
17.(12分)某地区试行高考考试改革:在高三学年中举行5次统一测试,学生如果通过其中2次测试即可获得足够学分升上大学继续学习,不用参加其余的测试,而每个学生最多也只能参加5次测试.假设某学生每次通过测试的概率都是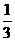 ,每次测试时间间隔恰当,每次测试通过与否互相独立.
,每次测试时间间隔恰当,每次测试通过与否互相独立.
(1)求该学生考上大学的概率.
(2)如果考上大学或参加完5次测试就结束,记该生参加测试的次数为ξ,求ξ的分布列及ξ的数学期望.
16.(12分)已知:函数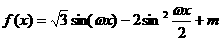 的周期为
的周期为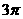 ,且当
,且当 时,函数
时,函数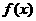 的最小值为0.
的最小值为0.
(1)求函数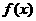 的表达式;
的表达式;
(2)在△ABC中,若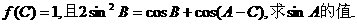
11.观察:①tan10°·tan20°+tan20°·tan60°+tan60°·tan10°=1;
②tan15°·tan25°+tan25°·tan50°+tan50°·tan15°=1;
③tan13°·tan27°+tan27°·tan50°+tan50°·tan13°=1.已知以上三式成立且还有不少类似的等式成立,请你再写出一个这样的式子:______________.
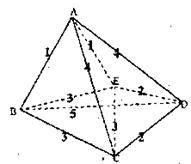 12.有一地球同步卫星A与地面四个科研机构B、C、
12.有一地球同步卫星A与地面四个科研机构B、C、
D、E,它们两两之间可以相互接发信息,由于功
率有限,卫星及每个科研机构都不能同时向两处
发送信息(例如A不能同时给B、C发信息,它
可先发给B,再发给C),它们彼此之间一次接发
信息的所需时间如右图所示.则一个信息由卫星
发出到四个科研机构都接到该信息时所需的最短
时间为________.
13(选做题).在极坐标系中,以ρcosθ+1=0为准线,(1,0)为焦点的抛物线的极坐标方程为_______________.
14(选做题).不等式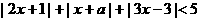 的解集非空,则
的解集非空,则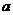 的取值范围为___________.
的取值范围为___________.
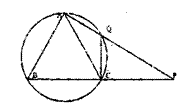 15(选做题).在圆内接△ABC中,AB=AC=
15(选做题).在圆内接△ABC中,AB=AC=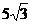 ,
,
Q为圆上一点,AQ和BC的延长线交于点P(如
图),且AQ:QP=1:2,则AP=_________.
10.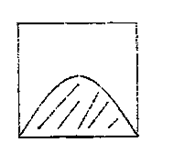 如图所示,墙上挂有一块边长为2的正方形木板,上面画有振幅为1的正弦曲线半个周期的图案(阴影部分).某人向此板投镖,假设每次都能击中木板并且击中木板上每个点的可能性都一样,则他击中阴影部分的概率是_________.
如图所示,墙上挂有一块边长为2的正方形木板,上面画有振幅为1的正弦曲线半个周期的图案(阴影部分).某人向此板投镖,假设每次都能击中木板并且击中木板上每个点的可能性都一样,则他击中阴影部分的概率是_________.
9.已知A(2,1),B(-2,3),以AB为直径的圆的方程为______________.
8.已知双曲线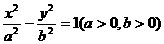 的右顶点为E,双曲线的左准线与该双曲线的两渐近线的交点分别为A、B两点,若∠AEB=60°,则该双曲线的离心率
的右顶点为E,双曲线的左准线与该双曲线的两渐近线的交点分别为A、B两点,若∠AEB=60°,则该双曲线的离心率 是 ( )
是 ( )
A.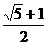 B.2 C.
B.2 C.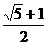 或2 D.不存在
或2 D.不存在
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com