
题目列表(包括答案和解析)
2.如图,正三角形ABC与直角三角形BCD成直二面角,且∠BCD=90°,∠CBD=30°.
 (1)求证:AB⊥CD;
(1)求证:AB⊥CD;
(2)求二面角D-AB-C的大小;
答案与提示:(2)arctan
3 空间角
例1、如图1,设ABC-A B
B C
C 是直三棱柱,F是A
是直三棱柱,F是A B
B 的中点,且
的中点,且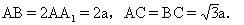
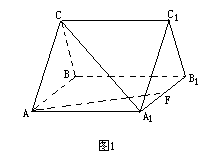

(1)求证:AF⊥A C; (2)求二面角C-AF-B的大小.
C; (2)求二面角C-AF-B的大小.
解:(1)如图2,设E是AB的中点,连接CE,EA .由ABC-A
.由ABC-A B
B C
C 是直三棱柱,知AA
是直三棱柱,知AA ⊥平面ABC,而CE平面ABC,所以CE⊥AA
⊥平面ABC,而CE平面ABC,所以CE⊥AA ,
,
∵AB=2AA =2a,∴AA
=2a,∴AA =a,AA
=a,AA ⊥AE,知AA
⊥AE,知AA FE是正方形,从而AF⊥A
FE是正方形,从而AF⊥A E.而A
E.而A E是A
E是A C在平面AA
C在平面AA FE上的射影,故AF⊥A
FE上的射影,故AF⊥A C;
C;
(2)设G是AB 与A1E的中点,连接CG.因为CE⊥平面AA
与A1E的中点,连接CG.因为CE⊥平面AA B
B B,AF⊥A
B,AF⊥A E,由三垂线定理,CG⊥AF,所以∠CGE就是二面角C-AF-B的平面角.∵AA
E,由三垂线定理,CG⊥AF,所以∠CGE就是二面角C-AF-B的平面角.∵AA FE是正方形,AA
FE是正方形,AA =a,
=a,
∴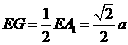 ,
∴
,
∴ ,
,
∴tan∠CGE=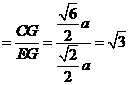 ,∠CGE=
,∠CGE=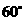 ,从而二面角C-AF-B的大小为
,从而二面角C-AF-B的大小为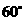 。
。
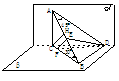
例2、 一条长为2的线段夹在互相垂直的两个平面a、b之间,AB与a成45o角,与b成 角,过A、B两点分别作两平面交线的垂线AC、BD,求平面ABD与平面ABC所成的二面角的大小.
角,过A、B两点分别作两平面交线的垂线AC、BD,求平面ABD与平面ABC所成的二面角的大小.
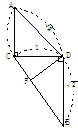
以CD为轴,将平 以AB为轴,将平

 面BCD旋转至与
面BCD旋转至与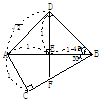 面ABD旋转至与
面ABD旋转至与
平面ACD共面 平面ABC共面
图 1 图 2 图 3
解法1、过D点作DE⊥AB于E,过E作EF⊥AB交BC于F(图1),连结DF,则∠DEF即为二面角D-AB-C的平面角.
为计算△DEF各边的长,我们不妨画出两个有关的移出图.在图2中,可计算得DE=1,EF=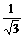 ,BF=
,BF=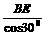 =
=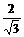 .在移出图3中,
.在移出图3中,
∵ cosB=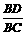 =
=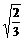 ,
,
在△BDF中,由余弦定理:
DF 2=BD 2+BF 2-2BD ﹒ BF ﹒ cosB
=(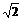 )2+(
)2+(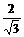 )2 -2
)2 -2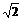 ﹒
﹒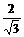 ﹒
﹒ 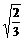 =
=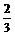 .
.
(注:其实,由于AB⊥DE,AB⊥EF,∴ AB⊥平面DEF,∴ AB⊥DF.
又∵ AC⊥平面b, ∴ AC⊥DF. ∴ DF⊥平面ABC, ∴ DF⊥BC,即DF是Rt△BDC斜边BC上的高,于是由BC ﹒ DF=CD ﹒BD可直接求得DF的长.)
在△DEF中,由余弦定理:
cos∠DEF=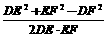 =
=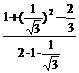 =
=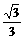 .
.
∴ ∠DEF=arccos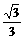 .此即平面ABD与平面ABC所成的二面角的大小.
.此即平面ABD与平面ABC所成的二面角的大小.
解法2、过D点作DE⊥AB于E,过C作CH⊥AB于H,则HE是二异面直线CH和DE的公垂线段,CD即二异面直线上两点C、D间的距离.运用异面直线上两点间的距离公式,得:
CD 2=DE 2+CH 2+EH 2-2DE CH cosq (*)
(注:这里的q是平面ABD与平面ABC所成的二面角的大小,当0<q o≤90o,q 亦即异面直线CH与DE所成的角;当90o<q <180o,异面直线所成的角为180o-q .)
∵ CD=DE=1,CH=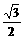 ,HE=
,HE=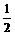 ,
,
从而算得 cosq=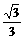 , ∴ q=arccos
, ∴ q=arccos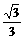 .
.
例3、如图1,直三棱柱ABC-A B
B C
C 的各
的各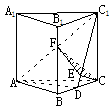 条棱长都相等,
条棱长都相等,
D为棱BC上的一点,在截面ADC 中,若∠ADC
中,若∠ADC =
= ,
,
求二面角D-AC1-C的大小.
解:由已知,直三棱柱的侧面均为正方形, 图 7
∵ ∠ADC1=90o,即AD⊥C1D.又CC1⊥平面ABC,
∴ AD⊥CC1. ∴ AD⊥侧面BC1,∴ AD⊥BC, 图1
∴ D为BC的中点.
过C作CE⊥C1D于E,∵ 平面ADC1⊥侧面BC1,
∴ CE⊥平面ADC1.取AC1的中点F,连结CF,则CF⊥AC1.
连结EF,则EF⊥AC1(三垂线定理)
∴ ∠EFC是二面角D-AC1-C的平面角.
在Rt△EFC中,sin∠EFC=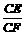 . ∵ BC=CC1=a
. ∵ BC=CC1=a
易求得 CE=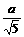 ,CF=
,CF=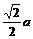 .
.
∴ sin∠EFC= , ∴ ∠EFC=arcsin
, ∴ ∠EFC=arcsin .
.
∴ 二面角D-AC1-C的大小为arcsin .
.
例4、(2004年北京春季高考题)如图,
四棱锥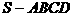 的底面是边长为1的正方形,
的底面是边长为1的正方形,
 图(1)
图(1)
SD垂直于底面ABCD,SB=√3。
(I)求证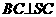 ;
;
(II)求面ASD与面BSC所成二面角的大小;
(III)设棱SA的中点为M,求异面直线DM与SB所成角的大小。
(Ⅳ)求SD与面SAB所成角的大小。
分析:本小题主要考查直线与平面的位置关系等基本知识,考查空间想象能力、逻辑思维能力和运算能力。
(I)证明:如图1
∵底面ABCD是正方形 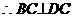
SD⊥底面ABCD  DC是SC在平面ABCD上的射影
DC是SC在平面ABCD上的射影
由三垂线定理得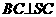
(II)解:SD⊥底面ABCD,且ABCD为正方形
 可以把四棱锥
可以把四棱锥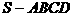 补形为长方体
补形为长方体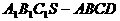 ,如图2
,如图2
面ASD与面BSC所成的二面角就是面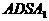 与面
与面 所成的二面角,
所成的二面角,
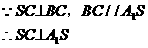
又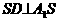
 为所求二面角的平面角
为所求二面角的平面角
在 中,由勾股定理得
中,由勾股定理得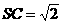 在
在 中,由勾股定理得
中,由勾股定理得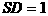
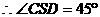 即面ASD与面BSC所成的二面角为
即面ASD与面BSC所成的二面角为
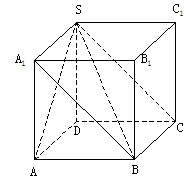
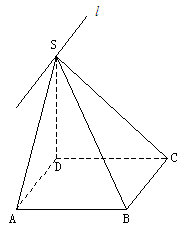
图2 图3
(III)解:如图3 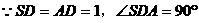
 是等腰直角三角形 又M是斜边SA的中点
是等腰直角三角形 又M是斜边SA的中点
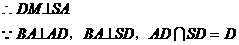
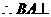 面ASD,SA是SB在面ASD上的射影
面ASD,SA是SB在面ASD上的射影
由三垂线定理得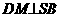
 异面直线DM与SB所成的角为
异面直线DM与SB所成的角为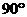
(Ⅳ) 45°
练习:1.设△ABC和△DBC所在的两个平面互相垂直,且AB=BC=BD,∠ABC=
∠DBC=120º.求:
(1).直线AD与平面BCD所成角的大小.
(2).异面直线AD与BC所成的角.
(3) .二面角A-BD-C的大小.
答案:(1)45°(2)90°(3)180°-arctan2
1.在四棱锥P-ABCD中,已知PD⊥底面ABCD,底面ABCD为等腰梯形,且∠DAB=60°,AB=2CD,∠DCP=45°,设CD=a.
(1)求四棱锥P-ABCD的体积.
(2)求证:AD⊥PB.
答案与提示:(1) a3
22.(本小题满分14分)
定义在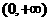 的三个函数f(x)、g(x)、h(x),已知f(x)=lnx , g(x)=
的三个函数f(x)、g(x)、h(x),已知f(x)=lnx , g(x)= 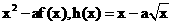 ,且g(x)在[1,2]为增函数,h(x)在(0,1)为减函数.
,且g(x)在[1,2]为增函数,h(x)在(0,1)为减函数.
(I)求g(x),h(x)的表达式;
(II)求证:当x>1时,恒有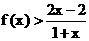 ;
;
(III)把h(x)对应的曲线 向上平移6个单位后得曲线
向上平移6个单位后得曲线 ,求
,求 与g(x)对应曲线
与g(x)对应曲线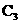 的交点个数,并说明道理.
的交点个数,并说明道理.
21.(本小题满分12分)
已知椭圆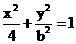 的焦点在x轴上,其右顶点关于直线x-y+4=0的对称点在直线
的焦点在x轴上,其右顶点关于直线x-y+4=0的对称点在直线
l: 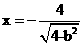 上.
上.
(I)求椭圆方程;
(II)过椭圆左焦点F的直线交椭圆于A、B两点,交直线l于点C,设O为坐标原点,且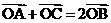 ,求
,求 的面积.
的面积.
20.(本小题满分12分)
如图,在四棱锥P-ABCD中,PA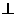 平面ABCD,底面ABCD是直线梯形,
平面ABCD,底面ABCD是直线梯形,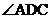 为直角,
为直角,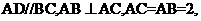 G是
G是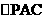 的重心,E为PB中点,F在线段BC上,且CF=2FB.
的重心,E为PB中点,F在线段BC上,且CF=2FB.
(I)证明:FG//平面PAB;
(II)证明:FG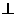 AC;
AC;
(III)求二面角P-CD-A的一个三角函数值,使得FG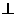 平面AEC
平面AEC
19.(本小题满分12分)
已知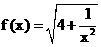 ,数列
,数列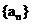 的前n项和为
的前n项和为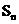 ,点
,点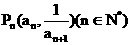 在曲线y=f(x)上,且
在曲线y=f(x)上,且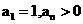 .
.
(I)求数列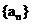 的通项公式
的通项公式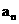 ;
;
 (II)数列
(II)数列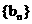 的首项
的首项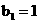 ,前n项和为
,前n项和为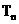 ,且
,且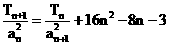 .求数列
.求数列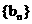 的通项公式
的通项公式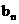 .
.
12.95,13.95)中的概率;
(III)根据样本,对总体的平均值进行估计.
13.7,12.7,14.7,13.8,13.3,12.5,13.5,13.6,13.1,12.6.
其分组情况如下:
(I)完成上面频率分布表;
(II)根据上表,在给定的坐标系中画出频率分布直方图,并根据样本估计总体数据落在
18.(本小题满分12分)
有同一型号的汽车100辆,为了解该型号汽车每耗油1L所行路程的情况,现从中随机抽出10辆在同一条件下进行耗油1L所行路程实验,得到如下样本数据(单位:km)
17.(本小题满分12分)
设函数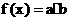 ,其中a=(2cosx,1),b=(cosx,
,其中a=(2cosx,1),b=(cosx, 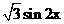 ),
),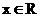 .
.
(I) 求f(x)的最大值;
(II)在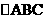 中,a、b、c分别是角A、B、C的对边,且
中,a、b、c分别是角A、B、C的对边,且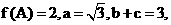 求b、c的值.
求b、c的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com