
题目列表(包括答案和解析)
2、对三角函数性质的考查总是与三角变换相结合.一般解题规律是先对三角函数关系式进行三角变换,使之转化为一个角的三角函数的形式,再利用换元法转化为对基本三角函数性质的研究.
1、三角变换基本解题方法:切割化弦,异名化同名,异角化同角,高次化低次,无理化有理.
常用的技巧:升幂降幂法、辅助元素法,“1”的代换法、利用倍角公式建立2α与α、α与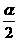 的关系、角的配凑等
的关系、角的配凑等
例5. 以平行六面体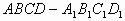 的任意三个顶点为顶点作三角形,从中随机取出2个三角形,则这2个三角形不共面的概率P为()
的任意三个顶点为顶点作三角形,从中随机取出2个三角形,则这2个三角形不共面的概率P为()
A. 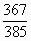 B.
B. 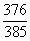 C.
C. 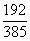 D.
D. 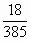
解析:此问题可分解成五个小问题:
(1)由平行六面体的8个顶点可组成多少个三角形?
可组成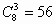 (个)三角形。
(个)三角形。
(2)平行六面体的8个顶点中,4点共面的情形共有多少种?
平行六面体的6个面加上6个对角面,共12个平面。
(3)在上述12个平面内的每个四边形中共面的三角形有多少个?
有 (个)
(个)
(4)从56个三角形中任取2个三角形共面的概率P等于多少?

(5)从56个三角形中任取2个三角形不共面的概率P等于多少?
利用求对立事件概率的公式,得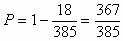 。
。
故选A。
点评:这道题以立体几何熟知内容为载体,构思巧妙,综合考查立体几何、排列组合、概率等基础知识,深入考查同学们的数学思维能力。本题的得分率较低,同学们的主要失误表现在以下两方面:(1)面对一个复杂的问题,缺乏明确的解题目标意识,不善于将其分解为若干个子问题;(2)漏掉平行六面体的6个对角面也是4点共面的情形,造成所求概率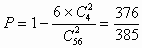 ,误选B。
,误选B。
例3. 过三棱柱任意两个顶点的直线共15条,其中异面直线有( )
A. 18对 B. 24对 C. 30对 D. 36对
解析:大家知道一个三棱锥可以确定3对异面直线,一个三棱柱可以组成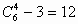 (个)三棱锥,则共有36对异面直线。故选D。
(个)三棱锥,则共有36对异面直线。故选D。
点评:利用熟知的立体图形来灵活转化,是处理异面直线配对问题的常用方法。
例4. 四棱锥的8条棱分别代表8种不同的化工产品,有公共点的两条棱所代表的化工产品在同一仓库中存放是危险的,没有公共点的棱所代表的化工产品在同一仓库中存放是安全的。现有编号为①②③④的四个仓库,用来存放这8种化工产品,则安全存放的不同方法总数为()
A. 96 B. 48 C. 24 D. 0

图3
解析:如图3,分别用1-8标号的棱表示8种不同的化工产品,易知可以两两放入同一仓库的情况如下(其实就是异面直线配对):
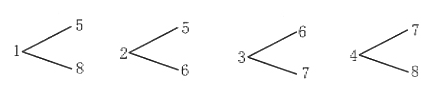
则8种产品安全存放有“(1,5)、(2,6)、(3,7)、(4,8)”和“(1,8)、(2,5)、(3,6)、(4,7)”两种可能,故所求的方法总数为 (种),应选B。
(种),应选B。
点评:这道实际应用题用四棱锥的8条棱的关系来研究化工产品的存放种数,体现了数学建模的思想。同学们在解决问题时,首先要将问题转化为四棱锥的8条棱之间的排列组合情况,然后再把四棱锥的8条棱分成4对异面直线。
例1. 不共面的四个定点到平面α的距离都相等,这样的平面α共有( )
A. 3个 B. 4个 C. 6个 D. 7个
解析:平面α可以分为两类:一类是在平面α的两侧各有两个点;另一类是在平面α的两侧分别有一个点和三个点。如图1,设E、F、G、H、M分别是AB、AC、AD、CD、BD的中点,过E、F、G三点的平面α满足题意,这样的平面有4个;又过E、F、H、M的平面α也满足题意,这样的平面有3个。故适合题设的平面α共有7个,应选D。
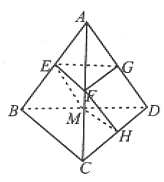
图1
例2. 在四棱锥P�ABCD中,顶点为P,从其他的顶点和各棱的中点中取3个,使它们和点P在同一平面上,不同的取法有()种。
A. 40 B. 48 C. 56 D. 62
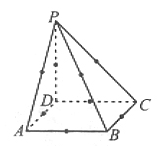
图2
解析:如图2,满足题设的取法可分为三类:
(1)在四棱锥的每个侧面上除点P外任取3点,有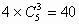 (种)不同的取法;
(种)不同的取法;
(2)在两个对角面上除点P外任取3点,共有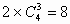 (种)不同的取法;
(种)不同的取法;
(3)过点P的每一条棱上的三点和与这条棱异面的棱的中点也共面,共有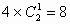 (种)不同的取法。
(种)不同的取法。
故不同的取法共有 (种)。
(种)。
点评:这类问题应根据立体图形的几何特点,选取恰当的分类标准,做到分类既不重复,也不遗漏。在例2中,最容易漏掉的是第(3)类,最易重复的也是第(3)类。
23、(一上P 第7题)求
第7题)求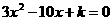 有两个同号且不相等实根的充要条件。
有两个同号且不相等实根的充要条件。
22、(一上 A第7题,
A第7题, B组第5题改编)解不等式:
B组第5题改编)解不等式:
(1)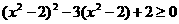 (2)
(2)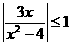
21、(一上P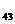 第1题)开校运动会时,高一(1)班共有28名同学参加比赛,有15人参加游泳比赛,有8人参加田径比赛,有14人参加球类比赛,同时参加游泳和田径比赛的有3人,同时参加游泳和球类比赛的有3人,没有人同时参加三项比赛,则同时参加田径和球类比赛的有
人;只参加游泳一项比赛的有 人.
第1题)开校运动会时,高一(1)班共有28名同学参加比赛,有15人参加游泳比赛,有8人参加田径比赛,有14人参加球类比赛,同时参加游泳和田径比赛的有3人,同时参加游泳和球类比赛的有3人,没有人同时参加三项比赛,则同时参加田径和球类比赛的有
人;只参加游泳一项比赛的有 人.
20、(一上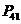 例2(2))“
例2(2))“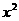 ≠
≠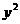 ”的等价写法是
。
”的等价写法是
。
19、(一上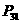 练习2)填空:
练习2)填空:
(1)命题“末位是0的整数,可以被5整除”的逆命题是
(2)命题“线段的垂直平分线上的点与这条线段两个端点的距离相等”的否命题是 。
(3)命题“到圆心的距离不等于半径的直线不是园的切线”的逆否命题是
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com