
题目列表(包括答案和解析)
4.若关于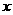 的不等式
的不等式 ≤
≤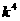 +4的解集是M,则对任意实常数
+4的解集是M,则对任意实常数 ,
,
总有( )
(A)2∈M,0∈M;
(B)2 M,0
M,0 M;
M;
(C)2∈M,0 M;
(D)2
M;
(D)2 M,0∈M.
M,0∈M.
2.在等差数列 中,若
中,若 ,
,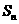 是数列的
是数列的 的前n项和,则
的前n项和,则 的值为( )
的值为( )
(A)48 (B)54 (C)60 (D)66

3如图,已知正六边形 ,下列向量的数量积
,下列向量的数量积
中最大的是( )
(A) (B)
(B)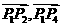
(C) (D)
(D)
1.已知集合 则集合
则集合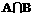 =( )
=( )
(A)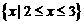 (B)
(B) (C)
(C) (D)
(D)
22.设二次函数f(x)=ax2+bx+c,(a,b,c∈R)满足下列条件:
①当x∈R时,f(x)的最小值为0,且f(x-1)=f(-x-1)成立;
②当x∈(0,5)时,x≤f(x)≤2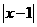 +1恒成立。
+1恒成立。
(1)求f(1)的值;
(2)求f(x)的解析式;
(3)求最大的实数m(m>1),使得存在实数t,只要当x∈ 时,就有f(x+t)≤x成立。
时,就有f(x+t)≤x成立。
21.某地西红柿从2月1日起开始上市,通过市场调查,得到西红柿种植成本Q(单位:元/102kg)与上市时间t(单位:天)的数据如下:
|
时间/t |
50 |
110 |
250 |
|
种植成本Q |
150 |
108 |
150 |
(1)根据上表数据,从下列函数中选取一个函数模型描述西红柿种植成本Q与上市时间t的变化关系: ,并说明选取的理由;
,并说明选取的理由;
(2)利用您选取的函数模型,求西红柿种植成本最低时的上市天数及最低种植成本.
20.如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动.
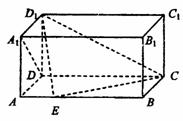 (1)证明:D1E⊥A1D
(1)证明:D1E⊥A1D
(2)AE等于何值时,二面角D1-EC-D的大小为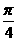
19. 已知函数 、
、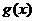 对任意实数x、y分别满足
对任意实数x、y分别满足
① ②
② 为正整数
为正整数
(1)求数列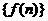 、
、 的通项公式;
的通项公式;
(2)设 的前n项和。
的前n项和。
18. A、B、C为△ABC的三内角,且其对边分别为a、b、c.若
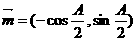 ,
,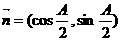 ,且
,且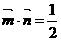 .
.
(1)求角A的大小;
(2)若a=2,三角形面积S=,求b+c的值.
17. 已知集合
(1)当m=3时,求
 ;
;
(2)若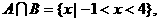 求实数m的值.
求实数m的值.
14.一个社会调查机构就某地居民的月收入调查10 000人,并根据所得数据画了样本的频率分布直方图(如下图)。为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10 000人中再用分层抽样方法抽出100人作进一步调查,则在(2 500,3 000)(元)月收入段应抽出
人。

15已知 ,点C在∠AOB内,且∠AOC=45°,设
,点C在∠AOB内,且∠AOC=45°,设 ,则
,则 等于
.
等于
.
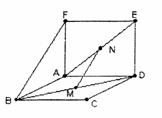 16. 如图,空间有两个正方形ABCD和ADEF,M、N分别为BD、AE的中点,则以下结论中正确的是
(填写所有正确结论对应的序号)
16. 如图,空间有两个正方形ABCD和ADEF,M、N分别为BD、AE的中点,则以下结论中正确的是
(填写所有正确结论对应的序号)
|
①MN⊥AD;
②MN与BF的是对异面直线;
③MN//平面ABF
④MN与AB的所成角为60°
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com