
题目列表(包括答案和解析)
5.已知三棱锥S-ABC的底面是正三角形,点A在侧面SBC上的射影H是△SBC的垂心,SA=a,则此三棱锥体积最大值是
A.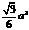 B.
B.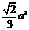 C.
C.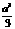 D.
D.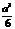
4.如图,一条螺旋线是用以下方法画成:△ABC是边长为1的正三角形,曲线CA1,A1A2,A2A3分别以A、B、C为圆心,AC、BA1、CA2为半径画的圆弧,曲线CA1A2A3称为螺旋线旋转一圈.然后又以A为圆心AA3为半径画圆弧……这样画到第n圈,则所得螺旋线的长度ln为
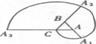 A.(3n2+n)
A.(3n2+n) B.(3n2-n+1)
B.(3n2-n+1) 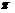
C.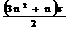 D.
D.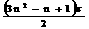
3.已知△ABC,若对任意t∈R,≥,则
A.∠A=900 B.∠B=900 C.∠C=900 D.∠A=∠B=∠C=600
2.设某等差数列的首项为a (a≠0),第二项为b.则这个数列中有一项为0的充要条件是
A.a-b是正整数 B.a+b是正整数C.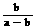 是正整数 D.
是正整数 D.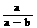 是正整数
是正整数
1.若复数z满足i (1+2i) z = 5,则z等于
A.2-i B.-2+i C.-2-i D.-1-2i
22.(本题满分14分)
已知关于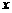 的方程
的方程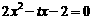 的两个根为
的两个根为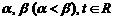 ,设函数
,设函数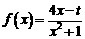 .
.
① 判断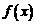 在
在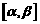 上的单调性;
上的单调性;
② 若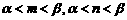 ,证明
,证明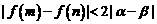 .
.
21.(本题满分12分)
已知直线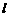 过椭圆E:
过椭圆E: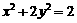 的右焦点
的右焦点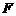 ,且与E相交于
,且与E相交于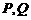 两点.
两点.
① 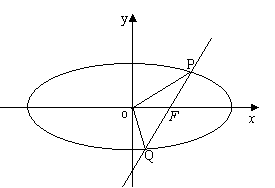 设
设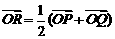 (
(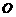 为原点),求点
为原点),求点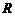 的轨迹方程;
的轨迹方程;
② 若直线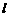 的倾斜角为
的倾斜角为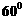 ,求
,求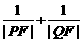 的值.
的值.
20.(本题满分12分)
 今有一张长2米宽1米的矩形铁板,如图,在四个角上分别截去一个边长为
今有一张长2米宽1米的矩形铁板,如图,在四个角上分别截去一个边长为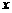 米的正方形后,沿虚线折起可做成一个长方体水箱(接口连接问题不考虑)。
米的正方形后,沿虚线折起可做成一个长方体水箱(接口连接问题不考虑)。
①
如果要使得水箱容积最大,则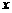 应取多少米?
应取多少米?
②
若要使水箱容积不大于4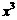 立方米的同时,又使得底面积最大以增加稳定性,
立方米的同时,又使得底面积最大以增加稳定性,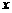 应取什么值?
应取什么值?
19.(本题满分12分)
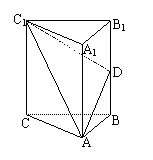
如图,在直三棱柱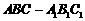 中,
中,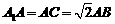 ,
, ,D为
,D为 的中点.
的中点.
①
 证明:平面
证明:平面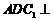 平面
平面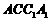 ;
;
②
求点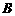 到平面的距离
到平面的距离 ;
;
③
求平面 与平面
与平面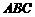 所成的二面角大小.
所成的二面角大小.
18.(本题满分12分)
已知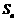 是数列
是数列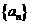 的前
的前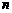 项和,
项和,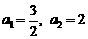 ,且
,且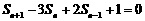 ,其中
,其中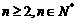 .
.
① 求数列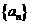 的通项公式
的通项公式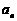 ;
;
② 计算 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com