3、下列说法中，不正确的是(　　 )

　　 A、函数的值域中的每个数都有原象

　　 B、定义域和值域分别相等的两函数是同一函数

　　 C、定义域和对应法则分别相同的两函数是同一函数

　　 D、函数的定义域只含一个元素，则值域也只有一个元素

2、下列四组函数中，表示同一函数是(　　　 )

　　 A、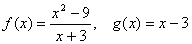

　　 B、

　　 C、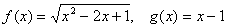

　　 D、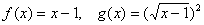

　　　　　　　　　　　 　　　　　　　　　A组

1、已知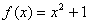，则f[f(－1)] 的值等于(　　　 )

　　 A、2　　　 B、3　　　 C、4　　　 D、5

4、评价：检验与评价结果是否符合实际。

例9.已知f(x+1)=x²-3x+2，

　 (1)求f(x)；

　 (2)求f(x-a)+f(x+a)

[探路]换元法：用凑法换元或设法换元。

[解法一]

　 (1)改写已知等式，并且凑法：

　　　 f(t+1)=t²-3t+2=(t+1)²-5t+1=(t+1)²-5(t+1)+6，

　　　 ∴f(x)=x²-5x+6

　 (2)f(x-a)+f(x+a)=(x-a)²-5(x-a)+6+(x+a)²-5(x+a)+6

　　　　　　　　　　　　　　 =2x²-10x+2a²+12

[解法二]

　　 (1)把已知等式改写为

　　　　　　　　　　 　f(t+1)=t²-3t+2

　　　　　　　 设 t+1=x，则t=x-1

　　　 f(x)=(x-1)²-3(x-1)+2=x²-5x+6

　　　 即f(x)=x²-5x+6

　　 (2)同“解法一”

[评注]

　　 解法一是“凑法”，解法二是“设法”，它们都是换元法。选用哪个方法要由题目的条件来确定，

　　 如本题解法二较好。但下面的例2用解法二(设法)却是不好的。

例10.已知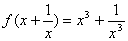，求f(x)和f(-3)。

[探路]

　　 用凑法换元。

[解]把已知式先改写，并用凑法：

　　 ∴

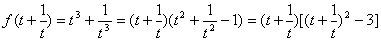
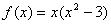
　　 ∴f(-3)=-3(9-3)=-18

[评注]

　　 本题用“设法”，即“设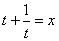，解出t”是不好的，请你试试看。

例11.求下列函数的定义域：

　　 (1)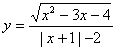；　 (2)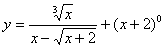

[解](1)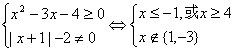

　　　 ∴函数的定义域是(-∞，-3)∪(-3，-1] ∪[4，+∞)。

　　　 (2)

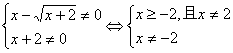
　　　　　 ∴函数的定义域是(-2，2)∪(2，+∞)

[评注]

　　 在(1)中，解|x+1|-2≠0得x≠1 , x≠-3，如果写成“x≠1，或x≠-3”，这是错误的；应写成

　　 “x≠1，且x≠3”。这是一个重要的逻辑思维问题，不要用错逻辑联结词“或”、“且”。写出

　　 上面的x{1，-3}是最好的。

　　 在(2)中，解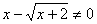时，先解方程，经检验x=-1是增根，应舍去。

　　 所以得x≠2。

　　 求定义域最关键问题是列出自变量可取值的充要条件组。在解析式上，目前应记准列条件组的下述

　　 法则：

　　 有分式--分母非零；

　　 有偶次根式--被开方式非负；

　　 有零指数幂--底非零。

例12.(1)已知y=f(x)的定义域是[-1，2]，求函数y=f(x+1)-f(x-1)的定义域。

　　　 (2)已知y=f(1-2x)的定义域是[-1，2]，求函数y=f(x)的定义域。

[探路]

　　 利用函数的符号意义来求其自变量的取值范围。先改写已知定义域的函数的自变量。

[解]

　　 (1)∵f(t)的定义域是[-1，2]，

　　　　 ∴-1≤t≤2。

　　　 对于函数y=f(x+1)-f(x-1)使f(t)有意义，应有

　　　　 ，

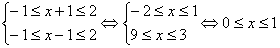　　 ∴函数y=f(x+1)-f(x-1)的定义域是[0，1]。

　　 (2)∵f(1-2t)的定义域是[-1，2]

　　 　 ∴-1≤t≤2

　　　　 ∴-3≤1-2t≤3

　　　　　 对于函数f(x)的自变量x=1-2t∈[-3，3]

　　 ∴函数y=f(x)的定义域是[-3，3]

[评注]

　　 本题就是“抽象问题”，求抽象函数的定义域要由函数符号的意义来确定，其关键是抓住“谁是自

　　 变量”，求定义域就是求自变量的取值范围。以本题之(2)为例：首先要弄清f(1-2x)和f(x)是两个

　　 不同的函数；因为它们的自变量都表示为x，为了防止混淆，把已知函数f(1-2x)改写为f(1-2t)，这

　　 样函数f(1-2t)的自变量为t∈[-1,2].所求函数f(x)的自变量为x，再由x=1-2t , t∈[-1 , 2]，求

　　 得x∈[-3，3]，即得f(x)的定义域。函数y=f(1-2t)是函数y=f(x)和函数x=1-2t的“复合”。中学

　　 所遇到的“抽象函数问题”就是这种复合函数的符号问题。

例13.求函数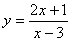的值域。

[探路]用“不等式法”或“反解法”。

[解法一]用“不等式法”：

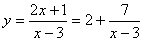
　　 由x≠3得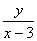≠0(即)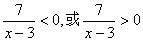

　　 ∴y≠2，即得函数y的值域：{y|y∈R，且y≠2}。

[解法二]用“反解法”，即“解x法”：

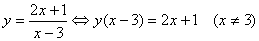
　　　　 　　　 ①

　　　　 关于自变量x的方程①有x≠3的解y≠2，

　　　　 ∴函数y的值域是{y|y∈R，且y≠2}

[评注]

　　 “不等式法”，已在前面说过，通过本例加以熟练。

　　 “反解法”就是把函数y=f(x) , x∈A(A是定义域)等价地化为关于自变量x的方程，求值域就是求

该方程在定义域上有解的充要条件。但不必求出x，只要用各种方法消去x，用y表出这个充要条件，即可

解得值域。当这个充要条件可用判别式表出，那么，这种“反解法”就叫做“判别式法”。当这个充要条

件不能用判别式表出，即是判别式法失效！

例14.求函数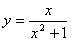的值域。

[探路]用“判别式法”

[解]该函数的定义域A=R

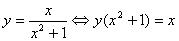
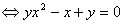　　　　　　　 　 　　　　　　　 ①

　 (1)当y=0时，①x=0∈A(定义域)，∴有y=0　

　 (2)当y≠0时，①有实数解△=1-4y²≥0(y≠0)

　 　　 Û。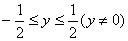

　　　 由(1)和(2)，得函数值域为[]。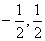

[评注]

　　 判别式法应用在二次方程中，所以应注意讨论方程①是否为二次方程，因此本题要分类讨论。

　　 本题“判别式法”有效，是因为二次方程①的根x∈R，没有限制。对于根x有限制的二次方程，△≥0

只是有实数根的必要条件，还要补加其它条件，使之成为充要条件才能求得值域，否则，要改用其他方法。

例15.求函数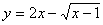的值域。

[探路]用换元法，设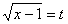，则x可用t的有理式表示，从而化为二次函数的值域问题。

[解]设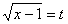，则t∈[0，+∞)，x=1+t²

　　　 ∴

　　　 ∴

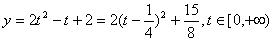
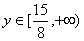
　　　 ∴函数的值域是[)。

[评注]

　　 用换元法，必须注意：不但解析式要完全化为新元的函数，而且要求出新元的取值范围(新函数的定

　　 义域)，即建立完整的新函数。如本例的新函数是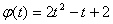，t∈[0，+∞]，否则，换元不等

　　 价，容易造成错误。

例16.x为何值时，|x-1|+|x-2|+|x-3|+|x-5|的值最小？并求出这个最小值。

[探路]

　　 显然，这是求函数。

　　　 f(x)=|x-1|+|x-2|+|x-3|+|x-5|

　　 的值域问题。用分类法(零点划分)是可以解决的，但要分为五种情况(分段函数)，太麻烦了，

　　 于是想用图象法来解，试试看，能不能非常简单，还有没有更妙的解法？

[解法一]

　　 (图象法)这个函数的图象是折线，其最小值必在折点上取得，于是计算四个折点的函数值：

　　 f(1)=7 , f(2)=5 , f(3)=5 , f(5)=9

　　 ∴f(x)的最小值为5，当x∈[2，3]时取得。

[解法三](利用绝对值的几何意义)画数轴：

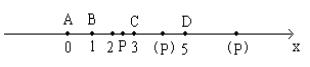
　　 设动点P的坐标为x，A、B、C、D的坐标分别为1、2、3、5，则f(x)=|x-1|+|x-2|+|x-3|+|x-5|

　　　 　　　　　　　　　　　　　　　　　　　　　　　 　=|PA|+|PB|+|PC|+|PD|=d

　　 由图可知，当点P在线段BC上时，取得d₀=|BC|+|AD|=1+4=5；当点P在线段BC的两侧延长线上时d>d₀，

　　 ∴当x∈[2，3]时，取得f(x)_min=5。

[评注]解法一是图象法，但无需画图，其图象是开口向上的折线，在解题者的想象之中。

　　 　解法二是“图解法”--画数学式的几何图，图解法包括图象法。由本题，我们看到图解法包括：

　　 (1)图象法；(2)图示法--画几何图或示意图

　　 　　　 图解法是数形结合法。

3、求解；

2、建立目标函数，如本例目标函数是求最值的矩形面积；

例1：下列对应是不是从A到B的映射？是不是函数？

　　 (1)A=(－∞,+∞)，B=(0，+∞),　 f∶x→y=|x|

　　 (2)A={x|x≥0}, B=R, f∶x→y, y²=x.

　　 (3)A={x|x≥2, x∈Z}, B={y|y≥0, y∈Z}, f∶x→y=x²-2x+2.

　　 (4)A={平面α内的矩形}，B={平面α内的圆}，f∶作矩形的外接圆。

[探路]　

　　 按映射的特点：A中每一元素都有象，且象唯一来判别；按函数的特点；A、B都是非空数集的映射来

　　 判别。

[解]

　　 (1)不是映射，因为0∈A，但|0|=0∈B，当然，(1)更不是函数。

　　 (2)不是映射，更不是函数。因为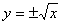，当x>0时，元素x的象不唯一。

　　 (3)是映射。因为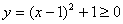，又当x∈A时，y∈Z，所以(3)是映射。又因为A、B都是数集，

　　　　 所以(3)也是函数。

　　 (4)是映射。因为每一个矩形都有唯一的外接圆，即A中每一元素在B中都有唯一的象，所以

　　　 (4)是映射。但A、B不是数集，所以不是函数。

例2：已知映射f∶A→B，其中，集合A={-3，-2，-1，1，2，3，4}，集合B的元素都是A中元素在映射f下

　　 的象，且对任意的a∈A，在B中和它对应的元素是|a|，则集合B中元素的个数是(　　　 )

　　 A、4　　　 B、5　　　 C、6　　　 D、7

[探路]该映射是函数，问题化为求函数的值域。

[解]已知映射f∶A→B是函数

　　 　 f(x)=|x|，定义域A={-3，-2，-1，1，2，3，4}，且B是值域，求值域，得

　　 　B={3，2，1，4}，其元素的个数是4，因此，选A。

[评注]

　　 用映射的概念来深刻理解函数，反之，用函数的方法来解映射的问题，这是把概念与操作相结合的现

　　 代观点，在本例，用具体的函数来操作映射是最快的算法，而不在概念中兜圈子。

例3：已知函数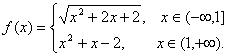

　　 求f[f(1)]和f[f(-1)]的值。

[探路]分段计算。

[解]∵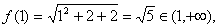

　　　 ∴

　　 　∵

　　　 ∴

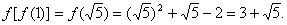
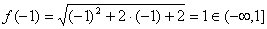
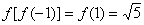
例4：下列哪组函数是同一函数？为什么？

　　 ①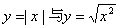

　　 ②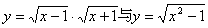

　　 ③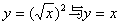

　　 ④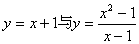

[解]

　　 ①是同一函数，因为对应法则等价：。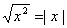

　　 ②不是同一函数，因为定义域不相等：前一函数的定义域是[1，+∞]后一函数的定义域是

　　　 。

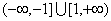　　 ③不是同一函数，因为定义域不相等：前一函数的定义域是[0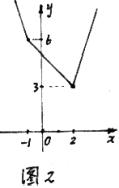，+∞)；后一函数的定义域是

　　 (－∞，+∞)。本题也可按值域不相等直接看出。

　　 ④不是同一函数。因为定义域不相等：前一函数的定义域为R；后一函数定义

　　　 域为。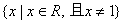

例5：作出函数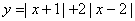的图象。

[探路]

　　 先把函数化为分段函数，再画图

[解]已知函数化为

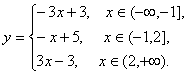
　　 其图象如图2。

[评注]

　　 这类函数的图象是折线，因此，还有画图快法：先求折点，即各绝对值等于零的点，如本题折点有

　　 两个：(-1，6)、(2，3)；再求一两个适当点画两边的射线，连折点间的线段，即成图。

例6：设集合A={a₁，a₂，a₃}，B={b₁，b₂}，

　　 (1)从A到B的映射有多少个？

　　 (2)从B到A的映射有多少个？

[探路]

　　 根据“什么叫映射”来做一个映射：先算每一元素的象有几种可能，然后就能算出共能做出多少个不

　　 同的映射。

[解]

　　 (1)作a₁的象有b₁或b₂2种方法，同样作a₂，a₃的象也各有2种方法，所以从A到B的映射，

　　　　 共有2×2×2=8个。

　　 (2)从B到A的映射共有3×3=9个。

例7：《中华人民共和国个人所得税法》规定，公民全月工资、薪金所得不超过800元的部分不必纳税，

　　 超过800元的部分为全月应纳税所得额。此项税款按下表分段累进计算。

　　 (1)某人今年十月份工薪为4000元，问他应纳税多少元？

　　 (2)某人去年十月份纳税26.78元，问他去年十月份的工薪为多少元？

[探路]利用分段函数进行计算。

[解](1)该人全月纳税所得额为

　　　 　4000元－800元=3200元

　　　 　他应纳税：500元×5%+1500元×10%+1200元×15%=355元。

　　 　 (2)工薪1300元应纳税：500元×5%=25元；

　　 　 　 　　工薪2800元应纳税：25元+1500元×10%=175元。

　　　　　　　 ∵26.78∈(25,175)，

　　　　　 ∴他去年十月份的工薪为1300元+(26.78－25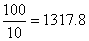)元×元。

例8：将长为l厘米的铁丝折成矩形，问怎样折才能使矩形的面积最大？并求出这个最大面积。

[探路]选取自变量，建立面积函数，注意定义域，求出值域，便得最大值。

[解]设折成的矩形的一边长为xcm，面积为Scm²，

　　 则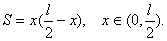　

　　 当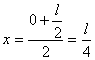时，取得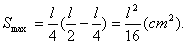

　　 ∴将铁丝折成边长为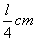的正方形时，面积最大，最大面积为

[评注]这种解决应用问题的方法叫“目标函数法”，其步骤是：

1、选取自变量，并确定定义域；

5.图象法。

[评注]

　　 函数的定义域和对应法则确定以后，值域就被完全确定，然而求出值域却是一个相当复杂的问题，没

　　 有包求所有函数值域的万能方法，只能靠自己不断地总结和发现它。今后，随着学习数学知识的丰富，

　　 解题也积累了经验，你将学会许多求值域的方法，但要注意总结和掌握最基本的通法。我们暂时学会

　　 上面的五个方法，并且只能采取“例中学”的方法。由于例题较多，暂不列举，请在下面的《B级》

　　 中学习求值域的范例。

4.反解法、判别式法。

3.换元法、配方法。