
题目列表(包括答案和解析)
2、 估算选择法
估算是用于解答选择题的一种简捷方法,它是指通过大体估值、合理猜想或特殊验证等手段,准确、迅速地选出答案的方法.充分体现了小题小(巧)做的解题策略.在近年高考的“多想少算”命题思想中,“估算法”更是解决此类问题的有效途径,常有以点估式(图)、以部分估整体、以范围估数值等.
例5(1999年全国高考题)如图1,在多面体ABCDEF中,已知面ABCD是边长为3的正方形,EF//AB,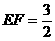 ,EF与面AC的距离为2,则多面体的体积为()
,EF与面AC的距离为2,则多面体的体积为()
A.  B. 5C. 6D.
B. 5C. 6D. 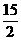
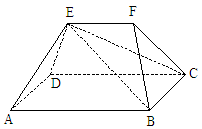
图1
分析:本题的背景是非典型的多面体,需对图形进行分解、组合.连EB、EC,得一个四棱锥E-ABCD和一个三棱锥E-BCF,结合选项可知:用易求的部分体积“四棱锥E-ABCD”估整体法,极其简捷.
解: 本题可用部分估整体法,连EB、EC,则易得
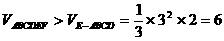
故排除A、B、C,应选D
评注:以部分估整体是指欲求结论由若干部分(或元素)构成时,研究易求的部分(或元素)而进行排除错肢,从而快速选答.
例6若四面体各棱长是1或2,且该四面体不是正四面体,则其体积的值不可能是 ( )
A、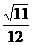
 B、
B、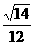 C、
C、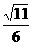 D、
D、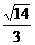
例7正方体的全面积是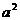 ,它的顶点都在球面上,这个球的表面积是()
,它的顶点都在球面上,这个球的表面积是()
A. 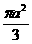 B.
B. 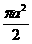 C.
C. 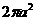 D.
D. 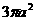
分析:此题如“不看选项,只看题干”,则变成普通的求解题,可以预见运算量不少,恐怕很难心算而得到结果,然而将“题目与四选项相结合”,用范围来估算,几乎人人都能一望而答--这就是估算法的魅力.
解:外接球的表面积,比起内接正方体的全面积来,自然要大一些,但绝不是它的约6倍(C)或约9倍(D),也不可能与其近似相等(A),故选B.
基于选择题的特点,解选择题有两条重要思路:一是肯定一支,二是否定三支 .下面例析如何运用此两条思路,进行选择题的快速选择
1、 直接选择法
直接从题设出发,通过推理和准确的运算得出正确的答案再与选择的答案支对照比较,从而判定正确选择支。它一般步骤是:计算推理、分析比较、对照选择。它又可分为两个层次:
①直接判定法
有些选择题结构简单,常可从题目已知入手,利用定义、定理、性质、公式直接指出正确答案。多用于解答有关基本概念或简单性质辨析的选择题。
②求解对照法
对于涉及计算或证明的选择题,有时可采用求解对照法。其基本思想是把选择题当作常规题来解,然后与题目选择支相对照,选出正确答案。
例3设有三个函数,第一个函数是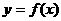 ,它的反函数是第二个函数,而第三个函数与第二个函数图象关于
,它的反函数是第二个函数,而第三个函数与第二个函数图象关于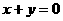 对称,那么第三个函数是 ( C )
对称,那么第三个函数是 ( C )
(A)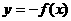 (B)
(B)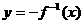 (C)
(C)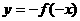 (D)
(D)
解: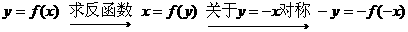 故选(C)
故选(C)
例4、设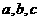 都是正数,且
都是正数,且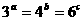 ,那么
( B )
,那么
( B )
(A)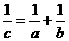 (B)
(B)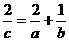 (C)
(C)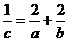 (D)
(D)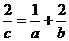
解:令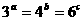 =k,取对数
=k,取对数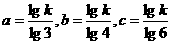 ,由
,由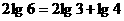
可得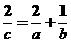 , 故选(B)
, 故选(B)
从命题的角度来看,一份数学试卷中的选择题都是用直接法求解,决不是一份好试卷,由于选择题不仅要担负检测“三基”的牢固程度,还担负着检测学生的思维敏捷灵活、快速的程度,故常要用到估算法、特例法、直觉思维法等等;从考试角度来看,一位同学解答一份试卷中的选择题都用直接法求解,往往导致“小题大作”,也决不会得到理想的分数,由于在解选择题过程中用时过多,就挤掉了后面考虑难题的时间,就是一种潜在丢分或隐含失分. 因此研究选择题的得分技巧必须做到:简捷快速.如何才能做到“简捷快速”,首先要了解选择题的三个特点:结构特征、担任角色及解法要求,然后才能有的放矢、抓住要害、获得简解.
选择题的结构特征与常规的解答题一样,有前提因素和结论因素,但更有自己的独特地方,可细分为四部分.
前提的组成是解题的信息源,它包含了三个部分:
⑴统一前提--所有的选择题的共同说明词,即“在每小题给出的四个选项中,只有一项符合题目要求的”. 也就是在四个选项中“有且只有一个正确”的单项选择题.
⑵具体前提--即题干,类似于解答题中的已知条件.
⑶选择前提--四个可供选择的答案,亦称选项,其中三个选项是错误的. 这是一个独特的条件,既有结论因素,又不象证明题那样明确指出,但确实有一个正确选项.
结论是第四部分,既简单又独特.
⑷选择结论--填上代号,就是根据“统一前提”、“具体前提”、“选择前提”找出结论的代号.
选择题的角色要求,对于知识要求包括了解、理解、掌握等三个层次,总体来说属于基本题,平均得分率0.7左右,具有单、多、广、活等特点,即内容比较单一、数量比较多、覆盖面比较广、题型(取材)比较活泼. 其作用是考查 基础知识的的是否理解,基本技能的是否熟练,基本运算是否准确,基本方法是否会用,考虑问题是否严谨,解题速度是否快捷.
据近年高考选择题命题特点是“多考一点想,少考一点算”,以及选择题的结构特征和知识特征,则其解法要求是要做到“小题小(巧)做”,避免“小题大(难)做”.否则就是潜在丢分或隐含失分.下面举例说明.
例1(2001年全国高考题) 过点A(1,-1)、B(-1,1)且圆心在直线x+y-2=0上的圆方程是( )
(A) (x-3)2+( y+1)2=4(B) (x+3)2+( y-1)2=4
(C) (x-1)2+( y-1)2=4 (D) (x+1)2+( y+1)2=4
解法1:(小题大做)
设圆的方程为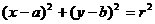 ,根据题意,得
,根据题意,得
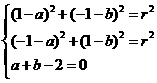 ,解得
,解得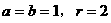 ,故选(C).
,故选(C).
解法2:(小题大做)
设圆的方程为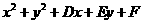 =0,根据题意,得
=0,根据题意,得
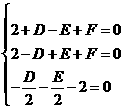 ,解得D=E=F=-2,故选(C).
,解得D=E=F=-2,故选(C).
评注解法1、2是利用圆的标准方程和一般方程求解与做一道解答题没有任何区别,选择题的特点体现不出来,是“小题大做”.
解法3:(小题小做)
因圆心在直线x+y-2=0上,设圆心为(a,2-a),又A、B在圆上,由圆的定义,有
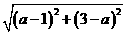 =
=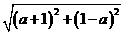
解得a=1,圆心为(1,1),排除(A)、(B)、(D),而选(C).
解法4:(小题小做)
由选项(B)、(D)的圆心坐标不在直线x+y-2=0上,故排除(B)、(D);又选项(A)的圆不过点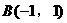 ,又排除(A),故选(C).
,又排除(A),故选(C).
评注 解法3、4对知识的理解程度及选择题的特点已有所理解,由于四个选项的半径相等,只是圆心不同,故只需考虑圆心坐标即可,有解法3;解法4是利用逆推验证法.
解法5: (小题巧做)
由选项知,只要估算出圆心所在的象限即可.显然圆心应在线段AB的垂直平分线(即一、三象限的角平分线)上,又在直线x+y-2=0上,画草图知,交点(即圆心)在第一象限内,故选(C).
例2在各项均为正数的等比数列{an}中,若a5a6=9,则log3a1+log3a2+…+log3a10=()
(A) 12(B) 10(C) 8 (D) 2+log35
解法1(小题难做)从已知条件中求出a1,q(或说an的表达式),从而逐项求出log3a1,log3a2,…,log3a10,再相加.由于条件中a5a6=9不能唯一确定一个数列,故此法无法办到.
解法2(小题大做)由已知9=a5a6=(a1q4)(a1
q5)= ,则
,则
a1a2…a10=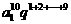 =
=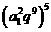 =310.
=310.
故原式=log3(a1a2…a10)=log3310=10,因而选(B).
评注此解法与做一道数列解答题没有任何区别,是典型的“小题大做”.
解法3(小题小做)由已知9=a5a6=a4a7=a3a8=a2a9=a1a10,
故原式=log3(a5a6)5=log3310=10,因而选(B).
评注此解法对等差数列知识的理解有所深化,但仍没有充分利用选择题的结构特点和回答方式上的特点.
解法4(小题巧做)由结论暗示,不管数列{an}的通项公式是什么(有无穷多个),答案都是唯一的,故只需取一个满足条件的特殊数列an=3,知选(B).
从上面两例可以看出,解题是有技巧可言,不同方法技巧的选择,会影响解题的速度. 小题巧(小)解能节省大量时间,能在一二分钟内解决问题, 甚至是十几秒. 如何才能做到此点,下面例析快速选择技巧.
8.在△ABC中,D、E分别是AB、AC的中点,用向量方法证明:DE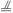
 BC.
BC.
7.已知ABCD为矩形,且AD=2AB,又△ADE为等腰直角三角形,F为ED的中点,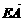 =e1,
=e1,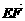 =e2以e1,e2为基底,试表示向量
=e2以e1,e2为基底,试表示向量 、
、 、
、 及
及 .
.
6.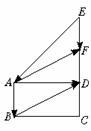 已知向量a=(x+3,x2-3x-4)与
已知向量a=(x+3,x2-3x-4)与 相等,其中A(1,2),B(3,2),求实数x的值.
相等,其中A(1,2),B(3,2),求实数x的值.
5.已知α、β是实数,a,b是不共线的向量,若(2α+β-4)a+(α-3β)b=0,则α=_________,β=_________.
4.D、E、F分别是△ABC边AB、BC、CA上的中点(如图),则等式
(1)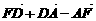 =0;
=0;
(2)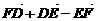 =0;
=0;
(3)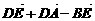 =0;
=0;
(4)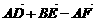 =0;
=0;
其中正确的是_________.
3.下面给出四个命题:
(1)对于实数m和向量a、b恒有:
m(a-b)=ma-mb;
(2)对于实数m,n和向量a,恒有:
(m-n)a=ma-na;
(3)若ma=mb(m∈R),则a=b;
(4)若ma=na(m,n∈R,a≠0),则m=n.
其中正确命题的个数是
A.1 B.2 C.3 D.4
2.已知△ABC中,AB=AC,DE是两腰上的中位线,则下列结论正确的是
A.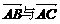 共线 B.
共线 B.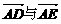 相等
相等
C.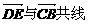 D.
D.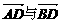 相等
相等
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com