3、复合法：例如，求函数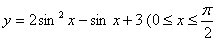)的值域。可用复合法：

　　　 设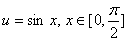，　　 ①

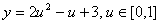　　　 则.　 ②

　　　 把函数②写成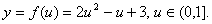

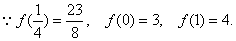
　　　 ∴函数y的值域是。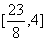

　　　 其中，把函数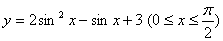写成①、②两个函数的复合，即

　　　 y=f(u), u=sinx。

　　　 这就是复合映射的方法，简称复合法。其实质是一种换元法。本节暂不深究，以后再学习。

问7.怎样求f(x)？举例说明。

[探路]

　　 求f(x)的方法应该是具体问题具体分析，依据问题的已知条件和问题类型，自我探索求法。这里，

　　 只能总结常用的方法，当然，这一总结也应该是“自我总结”，因为“自我总结”是学习的上策。

[解]求f(x)的常用方法是：

2、分段法：掌握分段函数。

　　 例如，把函数y=|x+1|-|x-2|化为分段函数是

1、一般表示法：解析法、图象法、列举法。

4、应该知道，函数的决定性要素是两个：定义域和对应法则，而值域是由定义域和对应法则确定的，

　　　 因而今后有“求函数的值域”的很多难题。因此，研究函数的任何问题都必须由定义域和对应法

　　　 则这两个独立要素下手。但很多人往往“忽视定义域”的错误。

问5：怎样判别两个函数是否为同一函数？

[解]要根据函数三要素来判别。

　　 判别法一(充要)：“定义域相同”且“对应法则等价”。

　　 判别法二(充要)：两个函数的图象完全重合，则两函数是同一函数。

　　 判别法三(必要)：

　　 (1)定义域不同，则函数不同。

　　 (2)值域不同，则函数不同。

问6：怎样表示函数？

[解]应掌握以下表示法：

3、值域C是B的子集，当B中的每一元素都有原象时，B=C。

2、函数符号y=f(x)表示“y是x的函数”，有的简记作函数f(x)。而f(a)表示自变量x=a(a∈A) 时

　　　 的函数值(象)。

1、函数是特殊的映射，特别仅在A、B是非空数集。函数、一一映射、映射、对应之间的关系，

　　　 如图1所示。

4、映射是一种特殊的“对应”。而“对应”与集合一样，也是原始概念，即无定义的，但可以“说

　　　 明”：对应是两个集合A与B的关系，通常以一个集合为主来考虑，对于A中的每一个元素来说，有

　　　 以下三种对应关系：

　　 (1)B中有唯一元素与之对应。

　　 (2)B中有多个元素(不是唯一)与之对应。

　　 (3)B中没有元素与之对应。

　　　　 映射就是第(1)种对应，而(2)、(3)两种对应不是映射。

问2：在映射f∶A→B中，什么叫“象”和“原象”？怎样判别一个对应是否是映射？试举一个正例和反例。

[解]在映射f∶A→B中，如果a∈A，b∈B，且元素a和元素b对应，那么，元素b叫做元素a的象，元素a叫

　　　 做元素b的原象，记作：f(a)=b。

　　　 判别一个对应是映射f∶A→B的要点是：

　　 ①A到B；

　　 ②A中每一个元素都有象，且象唯一

　　 例如，判别下面的对应是不是映射f∶A→B？

　　 (1)A={三角形}，B={圆}，对应法则f∶作三角形的外接圆。

　　 (2)A=B=R，对应法则f∶x→y=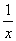

　　　 解：(1)是映射。(2)不是映射，因为0∈A，但0的象不存在。

问3：什么叫A到B上的一一映射？试举一个正例和反例。

[解]如果映射f∶A→B再满足：

　　　 那么这个映射叫做A到B上的一一映射。

　　　 例如，下面的映射f∶A→B是不是一一映射？

　　 (1)A={三角形}，B={圆}，对应法则f∶作三角形的外接圆。

　　 (2)A={x|x≥0}，B={y|y≥0}，对应法则f∶x→y=x².

　　 解：

　　 (1)不是一一映射，因为不同的三角形可以有同一个外接圆(一个圆的内接三角形有无数个)，

　　　　 即A中不同元素在B中有同一个象。

　　 (2)是一一映射，因为它满足一一映射的条件：

　　　　 ①设x₁,x₂∈A，且x₁≠x₂，则由x₁≥0，x₂≥0，x₁≠x₂Þy₁=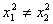=y₂；

　　　　 ②设任一个y₁∈B，则由x₁≥0Þy₁=x²Þx=。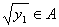

问4：什么叫函数(用映射回答)？函数的定义域、值域？指出函数的要素。

[解]

　　 如果A，B都是非空数集，那么A到B的映射f∶A→B就叫做A到B的函数，记作y=f(x)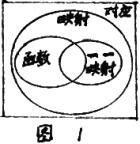(x∈A，y∈B)。

　　 原象的集合A叫做函数y=f(x)的定义域；象的集合C(CÍB)叫做函数y=f(x)

　　 的值域。

　　 函数的定义域、对应法则和值域，通常称为函数的三要素。

[评注]

3、在A到B的映射中，集合A中的每一个元素在B中都有“象”，且“象”唯一。

2、映射f∶A→B是有方向的，即从A到B，定义中只要求A中的每一个元素在B中有怎样的“象”？并不

　　　 要求B中的每一个元素在A中有怎样的对应。因此，“从A到B的映射”与“从B到A的映射”是不

　　　 同的。