
题目列表(包括答案和解析)
(三)两条直线平行与垂直的条件,两条直线所成的角,两条直线的交点,点到直线的距离
说明 这部分内容近年高考在填空、选择及解答题中都常考查到.
使用公式求l1到l2的角时,应注意k1、k2的顺序.过两直线交点的直线系方程中不 包括直线l2.
例3 光线由点(-1,4)射出,遇直线2x+3y-6=0被反射,已知反射光线过点(3 ,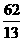 ).求反射光线所在直线方程.
).求反射光线所在直线方程.
解: 设(-1,4)点关于已知直线对称点为(x′,y′).
则点(-1,4)与点(x′,y′)的连线段被已知直线垂直平分,故可得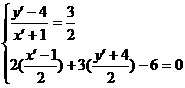 解得
解得 ,再由两点式可得所求直线方程为13x-26y+85=0.
,再由两点式可得所求直线方程为13x-26y+85=0.
(二)直线方程,直线的斜率,直线的点斜式、斜截式、两点式、截距式方程,直线方程的一 般形式
例2 直线xcosα-y+1=0的倾斜角的变化范围是 .
解 直线方程化为斜截式y=cosα·x+1,故k=cosα,
又-1≤k≤1,故倾角所取范围是[0,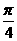 ]和[
]和[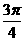 ,π]。
,π]。
(一)有向线段、两点间距离、线段的定比分点
例1 在△ABC中,A(4,1),B(7,5),C(-4,7),求∠BAC平分线的长.
解: 由两点距离公式求得│AB│=5,│AC│=10,设角平分线交BC于D(x,y),由角平分线性质得λ=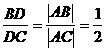 ,从而求得D(
,从而求得D(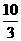 ,
,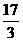 ),故可得│AD│=
),故可得│AD│=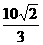 .
.
5.直线关于点的对称
直线关于点的对称直线一定是一条与已知直线平行的直线,由中点坐标公式可得
直线Ax+By+C=0关于点P(x0,y0)的对称直线方程是
A(2x0-x)+B(2y0-y)+C=0
即 Ax+By-(2Ax0+2By0+C)=0.
“直线关于直线”对称
(1)几种特殊位置的对称
已知曲线f(x,y)=0,则它:
①关于x轴对称的曲线是f(x,-y)=0;
②关于y轴对称的曲线是f(-x,y)=0;
③关于原点对称的曲线是f(-x,-y)=0;
④关于直线y=x对称的曲线f(y,x)=0;
⑤关于直线线y=-x对称的曲线
f(-y,-x)=0;
⑥关于直线x=a对称的曲线是
f(2a-x,y)=0;
⑦关于直线y=b对称的曲线是
f(x,2b-y)=0
4.点与直线的位置关系
点P(x0,y0)在直线Ax+By+C=0上的充要条件是
Ax0+By0+C=0.
点到直线的距离公式
点P(x0,y0)到直线Ax+By+C=0的距离是
d=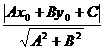
据此可推出:
(1)两平行线间的距离公式
两平行直线Ax+By+C1=0和Ax+By+C2=0间的距离为
d=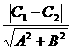 .
.
3.直线的方程
直线方程的几种形式
|
名称 |
已知条件 |
方程 |
说明 |
|
斜截式 |
斜率k纵截距b |
y=kx+bx |
不包括y轴和平行于y轴的直线 |
|
点斜式 |
点P 1(x1,y1)斜率k |
y-y1=k(x-x1) |
不包括y轴和平行于y轴的直线 |
|
两点式 |
点P1(x1,y1)和P2(x2,y2) |
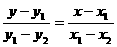 |
不包括坐标轴和平行于坐标轴的直线 |
|
截距式 |
横截距a纵坐标b |
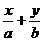 =1 =1 |
不包括坐标轴,平行于坐标轴和过原点的直线 |
|
一般式 |
- |
Ax+By+C=0 |
A、B不同时为0 |
两条直线的位置关系
当直线不平行于坐标轴时:
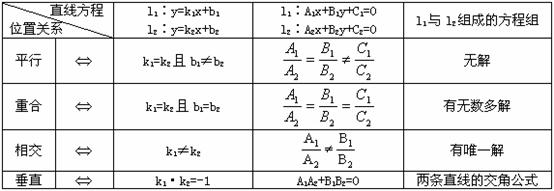
(1)直线l1到l2的角 直线l1依逆时针方向旋转到与l2重合时所转的角,叫做l1 到l2的角.
计算公式
设直线l1,l2的斜率分别是k1,k2,则
tgθ= (k1k2≠-1)
(k1k2≠-1)
(2)两条直线的夹角一条直线到另一条直线的角小于直角的角,即两条直线所成的锐角叫做两条直线所成的角,简称夹角.这时的计算公式为:tgθ=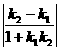
2.线段的定比分点
有向直线l上的一点P,把l上的有向线段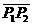 分成两条有向线段
分成两条有向线段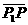 分成两条有向线段
分成两条有向线段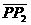 ,则
,则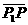 和
和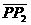 的数量之比
的数量之比
λ=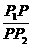
定比分点公式 若P1、P2两点坐标为(x1,y1),(x2,y2),点P(x,y)分有向线段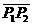 成定比
成定比
λ=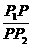 (λ≠-1),
(λ≠-1),
则P点坐标
x=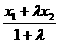 , y=
, y=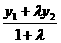 .
.
(1).中点公式 设P1(x1,y1),P2(x2,y2),则P1P2的中点P(x,y)的坐标是
x=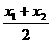 , y=
, y=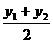 .
.
(2)三角形的重心公式 若△ABC的各顶点坐标分别为A(x1,y1),B(x2,y2),C(x3,y 3),则△ABC的重心G(x,y)的坐标是
x=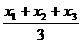 , y=
, y=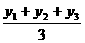
1.有向线段
一条有向线段的长度,连同表示它的方向的正负号,叫做有向线段的数量.有向线段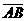 的数量用AB表示.
的数量用AB表示.
若有向线段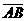 在数轴上的坐标为A(x1),B(x2),则
在数轴上的坐标为A(x1),B(x2),则
它的数量 AB=x2-x1
它的长度 |AB|=|x2-x1|
平面上两点间的距离 设P1(x1,y1),P2(x2,y2)是坐标平面上的任意两点,则 它们的距离
|P1P2|=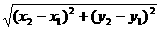
当P1P2⊥Ox轴时,|P1P2|=|y2-y1|;当P1P2⊥Oy轴时,|P1P2| =|x2-x1|;点P(x,y)到原点O的距离,|OP|=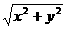 .
.
三角形的中线长公式
如图,AO是△ABC的BC边上的中线.则|AB|2+|AC|2

=2[|AO|2+|OC|2]
3.掌握两条直线平行与垂直的条件.能够根据直线的方程判定两条直线的位置关系.会求两条 直线的夹角和交点.掌握点到直线的距离公式.
2.理解直线斜率的概念,掌握过两点的直线的斜率的公式,熟练掌握直线方程的点斜式,掌 握直线方程的斜截式、两点式、截距式以及直线的一般式.能够根据条件求出直线的方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com