
题目列表(包括答案和解析)
1.已知直线l1:x+ay+1=0与直线l2:x-2y+2=0垂直,则a的值为 D
A.2
B.-2 C.-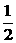 D.
D.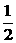
6、直线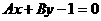 在y轴上的截距是-1,且它的倾斜角是直线
在y轴上的截距是-1,且它的倾斜角是直线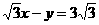 的倾斜角的2倍,则 ( )
的倾斜角的2倍,则 ( )
A.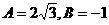 B.
B.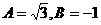 C.
C.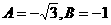 D.
D.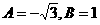
平行直线x-y+1 = 0,x-y-1 = 0间的距离是(B)
A.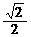 B.
B.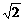 C.2 D.
C.2 D.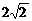
(三)解答题
16.已知平面α和不在这个平面内的直线a都垂直于平面β,求证a∥α.
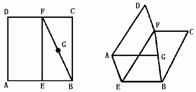
17.如图,正方形ABCD,E、F分别在AB、CD的中点,G为BF的中点,现将正方形沿EF折成 120°的二面角.求①异面直线EF和AG所成的角;②AG和平 面EBCF所形成的角.
18.圆柱底面半径是3,高是4,A与B分别是两底的圆周上的点,且AB=5,求异面直线AB与OO 1间的距离。
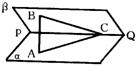
19.如图,已知二面角α-PQ-β为60°,点A和B分别在平面α和平面β内,点C在棱PQ 上,且∠ACP=∠BCP=30°AC=BC ①求证AB⊥PQ;②求直线PQ
在面ABC所成角的大小.
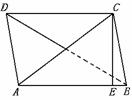
20.如图,设ABCD是矩形,沿对角线DB将ABDC折起,使点C在底面DAB上的射影E恰好落在 AB边上
(1)求证:平面ABC⊥平面ACD。
(2)若AB=2,BC=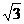 ,求二面角C-AD-B的大小及三棱锥C-ABD的体积。
,求二面角C-AD-B的大小及三棱锥C-ABD的体积。
(二)填空题
11.两条异面直线所成的角为θ,则cosθ的取值范围是 .
12.棱长为1的正方体,PA、PB、PC是共一个顶点P的三条棱,那么点P到平面ABC的距离是 .
13.从三棱锥六条棱的中点中,任选四个作为四边形的顶点.其中为平行四边形的个数有 个.
14.正方体ABCD所在平面与正方形ABEF所在平面成60°的二面角,则异面直线AD与BF所成角为 .
15.正四棱锥S-ABCD的高为2,底面边长为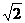 ,P、Q两点分别在线段BD和SC上 ,则P、Q两点的最短距离为
.
,P、Q两点分别在线段BD和SC上 ,则P、Q两点的最短距离为
.
(一)选择题
1.有下列四个命题:
(1)n条直线中,若任意两条都共面,则这n条直线都共面
(2)分别与两条异面直线都相交的两条直线是异面直线
(3)空间中有三个角是直角的四边形是矩形
(4)两条异面直线在同一平面内的射影不可能是平行线
其中,真命题的个数为( )
A.0 B.1 C.2 D.3
2.下列命题中,真命题是( )
A.若直线m、n都平行于平面α则m∥n
B.设α-l-β是直二面角,若直线m⊥l,则m⊥β
C.若m、n在平面α内的射影依次是一个点和一条直线,且m⊥n,则n在α内或n与α平行
D.若直线m、n是异面直线,若m与平面α平行,则n与α平行,则n与α相交
3.已知直线a、b和平面α,下列命题正确的是( )
(1)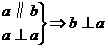 (2)
(2) 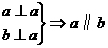
(3) 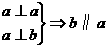 (4)
(4)
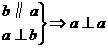
A.(1)(2) B.(1)(2)(3)
C.(1)(2)(4) D.(2)(3)(4)
4.设α、β是两个不重合的平面,m和l是两条不重合的直线,则α∥β的一个充分条( )
A.l α,m
α,m α且l∥β,m∥β
α且l∥β,m∥β
B.l α, m
α, m β且l∥m
β且l∥m
C.l⊥α,m⊥β,且l∥m
D.l∥α,m∥β且l∥m
5.四棱柱成平行六面体的充分但不必要条件是( )
A.底面是矩形 B.侧面是平行四边形
C.一个侧面是矩形 D.两个相邻侧面是矩形
6.二面角α-EF-β是直二面角,C∈EF,AC α,BC
α,BC β,如果∠ACF=30°,∠ACB=60° ,∠BCF=θ,那么cosθ的值等于,则( )
β,如果∠ACF=30°,∠ACB=60° ,∠BCF=θ,那么cosθ的值等于,则( )
A.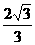 B.
B.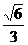 C.
C.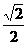 D.
D.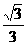
7.如图,有共同底边的等边△ABC和等边三角形BCD所在平面互相 垂直,则异面直线AB和CD所成角的余弦值为( )
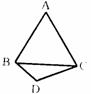
A.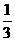 B.
B.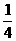 C.
C.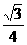 D.
D.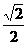
8.正方体ABCD-A1B1C1D1中截面AB1C和截面A1B1C所成的二面角的大小( )
A.45° B.60°
C.arccos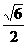 D.arccos
D.arccos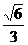
9.如图,BCDE是一个正方形,AB⊥平面CE,侧图中相互垂直的平面有( )
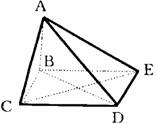
A.3组 B.6组
C.7组 D.8组
10.正方形ABCD-A1B1C1D1中,平面A1BC1与平面ABCD所成二面角的正弦值是( )
A.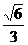 B.
B.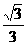 C.
C.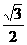 D.
D.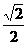
(二)空间直线和平面
例15 如果直线l是平面α的斜线,那么在平面α内( )
A.不存在与l平行的直线
B.不存在与l垂直的直线
C.与l垂直的直线只有一条
D.与l平行的直线有无穷多条
解 A正确。若存在l′ α且l′∥l,那么,或者l∥α或者l
α且l′∥l,那么,或者l∥α或者l α,均与“l是 α的斜线”矛盾
α,均与“l是 α的斜线”矛盾
由A.正确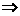 D.错误
D.错误
由三垂线定理知,B、C均不正确。
例16 如图(1),ABCD是正方形,E是AB中点,如 将△DAE和△CBE分别沿虚线DE和CE折起,使AE与BE重合,记A与B重合后的点为P,则面PCD与 面ECD所成的二面角为 度.
解:在图(2)上作PH⊥CD于H,设正方形ABCD的边长1.
易知PD=l,PC=l,∴H为DC中点.
又ED=EC.
∴EH⊥DC于H.
设∠PHE=θ,则θ为面PCD与面ECD所成二面角的大小.
在△PDC中,由PD=PC=DC=l,得PH=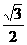 ,
,
在△EDC中,由EH=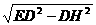
=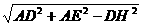 =l,
=l,
又P是A、B重合的点,故PE=AE=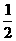 .
.
用余弦定理于△PHE,有
cosθ=cos∠PHE=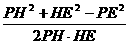
=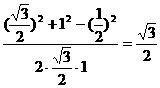 ,
,
由于θ∈(0,180°),得θ=30°.
应填30°.
例17 已知:如图,平面α∩平面β=直线a,α 、β同时垂直于平面 r,又同时平行于直线b.
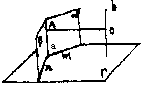
求证:(1)a⊥γ,(2)b⊥γ.
证明:(1)设α∩γ=m,β∩γ=n.
在直线a上任选不在平面γ上的点A,作AO⊥m于O,AO′⊥n于O′.
∵AO α,α⊥γ且α∩γ=m,AO⊥m,
α,α⊥γ且α∩γ=m,AO⊥m,
∴AO⊥γ(两面垂直,则在其中一个平面上且垂直于交线的直线必垂直于另一个面).同理AO ′⊥γ.
但平面γ外的点A在平面γ的射影唯一.
∴O和O′重合于m,n的交点.
即直线a⊥平面γ.
(2)∵b∥平面α,
∴存在b′ α,b′≠a;满足b∥b′.
α,b′≠a;满足b∥b′.
又b∥β,从而b′∥β.
因为平面α过b′且交平面β于a,
∴b′∥a,从而b∥a.
由a⊥γ,得b⊥γ.
例18 如果直线l,m与平面α、β、γ满足:l=β∩ r,l∥α
,m α,和m⊥γ,那么必有( )
α,和m⊥γ,那么必有( )
A.α⊥γ且l⊥m
B.α⊥γ且m∥β
C.m∥β且l⊥m
D.α∥β且α⊥γ
解:∵m α,m⊥γ,
α,m⊥γ,
∴γ⊥α,
∵l γ,m⊥γ,
γ,m⊥γ,
∴m⊥l.
即在题设的条件下必有γ⊥α且l⊥m.
应选A.
例19 如图1-37,在正三棱柱ABC-A1B1C1中,E ∈BB1,截面A1EC⊥侧面AC1.
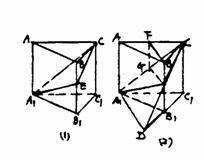
(1)求证:BE=EB1;
(2)若AA1=A1B1,求平面A1EC与平面A1B1C1所成二面角(锐角)的度数 .
注意:在下面横线上填写适当内容,使之成为(1)的完成证明,并解答(2).
证明:在截面A1EC内,过E作EG⊥A1C,G是垂足.
(Ⅰ)∵
∴EG⊥侧面AC1,取AC的中点F,连结BF、FG,由AB=BC得BF⊥FC.
(Ⅱ)∵
∴BF⊥侧面AC1,得BF∥EG,BF、EG确定一个平面,交侧面AC1于FC.
(Ⅲ)∵
∴BF∥EG,四边形BEGF是平行四边形,BE=FG.
(Ⅳ)∵
∴FG∥AA1,ΔAA1C∽ΔFGC,
(Ⅴ)∵
∴FG=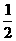 AA1=
AA1=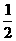 BB1,即BE=
BB1,即BE=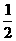 BB1,故BE=EB1.
BB1,故BE=EB1.
解:(1)(Ⅰ)∵面A1EC⊥侧面AC1,
(Ⅱ)∵而面ABC⊥侧面AC1,
(Ⅲ)∵BE∥侧面AC1,
(Ⅳ)∵BE∥AA1,
(Ⅴ)∵AF=FC.
(2)分别延长CE、C1B1交于点D,连结A1D.
∵EB1∥CC1,EB1=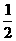 BB1=
BB1=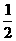 CC1,
CC1,
∴DB1=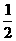 DC1=B1C1=A1B1,
DC1=B1C1=A1B1,
∵∠B1A1C1=∠B1C1A1=60°
∠DA1B1=∠A1DB1=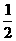 (180°-∠DB1A1)=30°
(180°-∠DB1A1)=30°
即DA1⊥A1C1
∵CC1⊥面A1C1B1,即A1C1在平面A1C1D上的射影,根据三垂线定理得DA1⊥A1C,
∴∠CA1C是所求二面角的平面角.
∵CC1=AA1=A1B1=A1C1,∠A1C1C=90°,
∴∠CA1C1=45°,即所求二面角为45°.
例20 在空间中,下列命题成立的是( )
A.过平面α外的两点,必有且只有一个平面与平面α垂直
B.若直线l上有两点到平面α的距离相等,则直线l必平行于平面α
C.若直线l与平面α内的无数多条直线垂直,则直线l必垂直于平面α
D.互相平行的两条直线在一个平面内的射影仍然是互相平行的两条直线
E.若点P到三角形的三条边的距离相等,则点P在该三角形所在平面内的射影必然是该三角形的内心
解:A不正确.若平面α外的两点A、B使直线AB⊥α,则过A、B两点且与α垂 直的平面有无数多个.
B不正确.设l和α交于点O,在l上取OA=OB,则A、B到平面α等距但直线AB 不平行于平面α.
C不正确.设l斜交α于O,在α内过O点作m⊥l,则α内与m平行的无数多条 直线都平行于l,但l与α不垂直.
D不正确.若互相平行的两直线a,b所确定的平面β⊥α,则a,b在α内的 射影是一条直线.
E正确.由三垂线定理易证明它的正确性.
例21 已知二面角α-AB-β的平面角是锐角θ,α内一点C到β的距离为3, 点C到棱的距离为4,那么tgθ的值等于( )
A.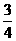 B.
B.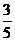 C.
C.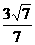 D.
D.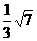
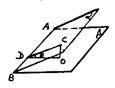
解:如图,CO⊥β于O,CD⊥AB于D,则CO=3,CD=4,∠CDO=θ,∠COD=90°.
∴tgθ=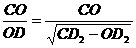
=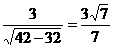 .
.
应选C.
例22 下列命题中,错误的是( )
A.若一直线垂直于一平面,则此直线必垂直于这平面上所有的直线
B.若一个平面通过另一个平面的一条垂线,则这两个平面互相垂直
C.若一条直线垂直于一个平面的一条垂线,则此直线平行于这个平面
D.若平面内的一条直线和这个平面的一条斜线的射影垂直,则它也和这条斜线垂直
解:B为两面垂直的一个判定定理.
A为线面垂直的性质定理.
C错误:设l⊥平面α,m∥l,若m α,则m∥α.
α,则m∥α.
应选C.
例23 下列四个命题中的真命题是( )
A.若直线l平面α内两条平行直线垂直,则l⊥α
B.若平面α内两条直线与平面β内两条直线分别平行,则α∥β
C.若平面α与直二角β-MN-r,棱MN交于点A,与二面角的面β,而r分别交于AB、AC,则∠BAC≤90°
D.以上三个命题都是假命题.
解:命题A不真
命题B不真;若这四条直线都平行,则有可能α∥β
命题C不真:
如图
BC2=BB′2+BC′2
=BB′2+CC′2+B′C2
=BB′2+CC′2+(B′A+C′A)2
>BB′2+CC′2+B′A′2+C′A2
=(BB′2+B′A2)+(CC′2+C′A2)
=BA2+CA2
∴∠BAC>90°
应选D.

[同步达纲练习]
(一)综合例题赏析
例11 设a、b是两条异面直线,那么下列四个命题中的假命题是( )
A.经过直线a有且只有一个平面平行于直线b
B.经过直线a有且只有一个平面垂直于直线b
C.存在分别经过直线a和b的两个互相平行的平面
D.存在分别经过直线a和b的两个互相垂直的平面
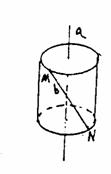
解:B是假命题,因为对于异面直线a、b,有时不存在过直线a且垂直于直线 b的平面.
如图,直线a是圆柱体的轴线,M、N分别为上下底圆周上的点且MN∥a,令b为直线MN, 则a,b为异面直线.
过直线a的平面以直线a为轴旋转,它们均与b不垂直.
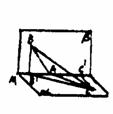
例12 已知异面直线a与b所成的角为50°,P为空间一定点,则过点P与a、b 所成的角都是30°的直线有且仅有( )
A.1条 B.2条 C.3条 D .4条
解:如图过点作PA∥a,PB∥b,则∠APB的异面直线a、b所成的平面角,由已知∠APB=50°.
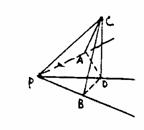
作∠APB的平分线PO,任取O∈PO,作CO⊥平面APB,令CB⊥PA于A,CB⊥PB于B,则由三垂线
定理知,OA⊥PA于A,OB⊥PB于B.
考虑C点沿平面APB的垂线OC自O点出发向上移动,易知∠CPB∈(25°,90°),
∴存在唯一点C使∠CPB=∠CPA=30°.
同理在垂线CO的下方还存在对称点C′,使∠C′PA=∠C′PB.
∴符合题设的直线有且只有两条.应选B.
例13 如图,正方体ABCD-A1B1C1D1中,直线BC1与直线AC( )
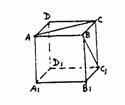
A.相交且垂直
B.相交但不垂直
C.异面且垂直
D.异面但不垂直
解:直线BC1和AC异面不垂直.
∵BC1∥AD1,
∴∠CAD1为异面直线AC,BC1所成的角.
在△CAD1中,CA=AD1=D1C.
∴∠CAD1=60°
即AC和BD1成60°角.
应选D.
例14 设a、b是异面直线,那么( )
A.必然存在唯一的一个平面同时平行于直线a和b
B.必然存在唯一的一个平面同时垂直于直线a和b
C.过直线a存在唯一的一个平面平行于直线b
D.过直线a存在唯一的一个平面垂直于直线b
解:A不正确.因为垂直于异面直线a、b公垂线的任何一个平面都与a、b平行 .
B不正确.若a⊥α,且b⊥α,则a∥b,此与a、b异面矛盾.
C正确.
D不正确.有时过直线a的所有平面都与直线b不垂直.
∴应选C.
(十)直线与平面的综合问题
例10已知如图,斜三棱柱ABC-A1B1C1的侧面A1ACC1与底面ABC垂直,∠ABC=90°,BC=2,AC=2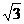 ,且AA1⊥A1C,AA1=A1C。
,且AA1⊥A1C,AA1=A1C。
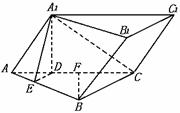
(1)求侧棱A1A与底面ABC所成角的大小。
(2)求侧面A1ABB1与底面ABC所成二面角的大小。
(3)求侧棱B1B和侧面A1ACC1的距离。
解 (1)作A1D⊥AC于D
由面A1ACC1⊥面ABC,得A1D⊥ABC
所以∠A1AD为A1A与面ABC所成的角
因AA1⊥A1C,AA1=A1C,
所以 ∠A1AD=45°为所求.
(2)作DE⊥AB于E,连结A1E,由A1D⊥面ABC得A1E⊥AB(三垂线定理)
则 ∠A1ED是面A1ABB1与面ABC所成的二面角的平面角.
由已知,AB⊥BC,得DE∥BC,又D是AC中点,BC=2,AC=2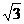
DE=1,AC=A1D=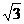 ,tg∠A1ED=
,tg∠A1ED=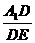 =
=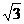
故 ∠A1ED=60°为所求.
(3)作BF⊥AC于F,由面A1ACC1⊥面ABC,知BF⊥面A1ACC1
因 B1B∥面A1ACC1
BF的长是B1B和面A1ACC1的距离
在Rt△ABC中,AB=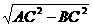 =2
=2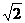
所以 BF=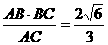
(九)点到直线、点到平面、直线与平面、平面与平面间的距离的定义及计算
例9 已知Rt△ABC中,∠A=90°,AB=a,AC=b,沿高AD折成直二面角(如图).(1)判断此时△ABC的形状;(2)求D到平面ABC的距离.
解:(1)DH⊥平面ABC,因DA、DB、DC两两互相垂直,故H为△ABC的垂心(证明略),AE⊥BC,由cosθ=cosθ1cosθ2,得cos∠ABE=cos∠ABD ·cos∠DBC.
∵∠ABD和∠DBC分别为Rt△BDC的锐角,故0<cos∠ABD,cos∠DBC<1,
∴0<cos∠ABE<1,即∠ABC为锐角,

同理可证∠ABC、∠CAB均为锐角,∴△ABC为锐角三角形.
(2)解法一:设D到平面ABC的距离为x.∵VD-ABC=VA-BDC得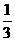 xSABC=
xSABC=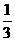 AD·S△BDC,
AD·S△BDC,
解出 x=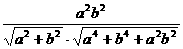 .
.
解法二:作AE⊥BC,AD⊥平面DBC,故DE⊥BC.BC⊥平面ADE,平面ADE⊥平面ABC,作DH⊥AE ,则DH是D到平面ABC的距离(以点线距离代替点面距离).在Rt△ADE中,DH是斜边AE上的高,解出
DH=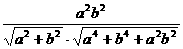 .
.
(八)二面角
例8 如图8(1),平面四边形ABCD中,AB=BC=CD=a,∠B=90°,∠C=135°,沿对 角线AC将四边形折成直二面角(如图8(2))
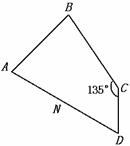
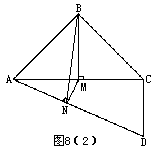
图8(1)
(1)求证:平面ABD⊥平面BCD;
(2)求平面ABD与平面ACD所成的角;
(3)求C到平面ABD的距离。
证明 (1)因B-AC-D是直二面角,CD⊥AC,
故 CD⊥平面ABC.CD⊥AB,AB⊥BC
AB⊥平面BCD,AB 平面ABD,
平面ABD,
所以 平面ABD⊥平面BDC。
解 (2)如图8(2)设M是AC的中点,则BC⊥AC,BM⊥平面ACD。作BN⊥AD,则MN⊥AD(三垂线定 理的逆定理).∠BNM为二面角B-AD-C的平面角。MN=AM·sin∠CAD=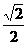 a·
a·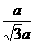 =
=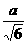 ,MB=
,MB=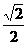 a.在Rt△BMN中,tg∠BNM=
a.在Rt△BMN中,tg∠BNM=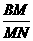 =
=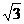 ,
,
则 二面角B-AD-C是60°的二面角。
(3)由(1)知,平面ABD⊥平面BCD,
作CH⊥BD,则CH⊥平面ABD。
CH=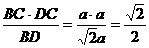 a,故C到平面ABD的距离为
a,故C到平面ABD的距离为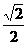 a.
a.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com