22.(本题满分14分)已知动点P与双曲线x²－y²=1的两个焦点F₁、F₂的距离之和为定值，且cosF₁PF₂的最小值为－。

(I)求动点P的轨迹方程;

(II)设M(0,－1)，若斜率为k(k≠0)的直线与P的轨迹交于不同的两点A、B，试求k的取值范围，使|MA|=|MB|；

(文)若直线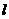:y=x+m与P的轨迹交于不同的两点A、B，且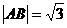，M(0，－1)，求M到直线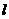的距离。

21．(本题满分12分)已知数列 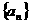的前项为a₁=2, 前n项和为S_n ,且对任意的n∈N₊，n≥2，a_n总是3S_n－4与2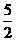－S_n－1的等差中项。

(1)求通项a_n;

(II)证明：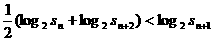

(III)(理)含b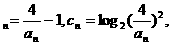T_n、R_n分别为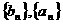的前n项和是否存在正整数n，使得T_n<R_n，若存在，请求出所有n的值，否则请说明理由。

(文) 设f(n)=a_n,g(n)=S_n, 解不等式：f²(n)>10－g(n)

20．(本题满分12分)设f(x)=x³+3x²+px, g(x)=x³+qx²+r，且y=f(x)与y=g(x)的图象关于点(0，1) 对称。

(I)求p、q、r的值；

(II)若函数g(x)在区间(0，m)上递减，求m的取值范围；

(III)若函数g(x)在区间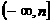　 上的最大值为2，求n的取值范围。

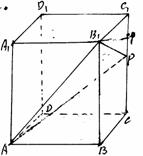
19．(本题满分12分)在正四棱柱ABCD－A₁B₁C₁D₁中，侧棱长是底面边长的2倍，P是侧棱CC₁上的任意一动点。

(I)求证：不论P在侧棱CC₁上何位置，总有BD⊥AP；

(II)若CC₁=3C₁P，求平面AB₁P与平面ABCD所成的二面角的余弦值；

(III)当点P在侧棱CC₁何处时，AP在平面B₁AC上的射影是∠B₁AC的平分线。

18．(本题满分12分)为了测试甲、乙两名射击运动员的射击水平，让他们各向目标靶射击10次，其中甲击中目标7次，乙击中目标6次。若再让甲、乙两人各自向目标靶射击3次，求：

(I)甲运动员恰好击中目标2次的概率是多少？

(II)(文)两名运动员都恰好击中目标2次的概率是多少？(结果保留两位有效数字)

(理)分别求甲、乙两名运动员击中目标次数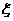、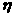的数学期望E、E的值。

17．(本题满分12分)已知锐角△ABC中，三个内角为A、B、C，两向量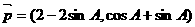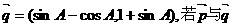，是共线向量。

(I)求∠A的大小；

(II)求函数y=2sin²B+cos()取最大值时，∠B的大小。

16．某大楼共有20层，有19人在第一层上了电梯，他们分别要去第2层至第20层，每层1人，而电梯只允许停 1次，可只使1人满意，其余18人都要步行上楼或下楼，假设乘客有向下走1层的不满意度为1，每向上走一层的不满意度为2，所有人的不满意度之和为S，为使S最小，电梯应当停在第___________层；

15．在平面几何中有：Rt△ABC的直角边分别为a,b，斜边上的高为h，则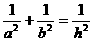。类比这一结论，在三棱锥P-ABC中，PA、PB、PC两点互相垂直，且PA=a，PB=b，PC=c，此三棱锥P-ABC的高为h，则结论为_______-。

14.某校有高中生1200人，初中生900人，老师120人，现用分层抽样的方法从所有师生中抽取一个容量为N的样本；已知从初中生中抽取人数为60人，那么N=__________。

13．设f(x)= x⁵－5x⁴+10x³－10x²+5x+1，则f(x)的反函数为 f^－1(x)=________。