
题目列表(包括答案和解析)
6. 以凸n边形的各边为直径作圆,使这个凸n边形必能被这n个圆面所覆盖,则n的最大值为( ) A.3 B.4 C.5 D.6
5.
如图,平面α中有△ABC和△A1B1C1分别在直线m的两侧,它们与m无公共点,并且关于m成轴对称,现将α沿m折成一个直二面角,则A,B,C,A1,B1,C1六个点可以确定的平面 个数为
( )
A.14 B.11 C.17 D.20
个数为
( )
A.14 B.11 C.17 D.20
4. 设实数m,n,x,y满足m2+n2=a,x2+y2=b,其中a,b为正常数且a≠b,那么mx+ny的最大值为 ( ) A. B. C. D.
3. 直线xcosθ+y+m=0(式中θ是△ABC的最大角),则此直线的倾斜角变化范围是( ) A.(-arctan) B.[0,,π) C.[0,] D.[0,]∪[π-arctan,π]
2. Sn和Tn分别是等差数列{an}和{bn}的前n项和,且对任意的自然数n都满足,那么= ( ) A. B. C. D.
1. 化简cos的值为 ( ) A.-1 B.1 C.- D.
3、由n个点和这些点之间的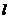 条连线段组成一个空间图形,其中
条连线段组成一个空间图形,其中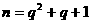 ,
, ,已知此图中任四点不共面,每点至少有一条连线段,存在一点至少有q+2条连线段。证明:图中必存在一个空间四边形(即由A,B,C,D和AB、BC、CD、DA组成的图形)。
,已知此图中任四点不共面,每点至少有一条连线段,存在一点至少有q+2条连线段。证明:图中必存在一个空间四边形(即由A,B,C,D和AB、BC、CD、DA组成的图形)。
2、设三角形的三边长分别是整数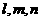 且
且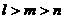 ,已知
,已知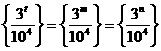 ,其中
,其中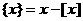 ,求这种三角形周长的最小值。
,求这种三角形周长的最小值。
1、过圆外一点P作圆的两条切线和一条割线,切点为A、B,所作割线交圆于C、D两点,C在P、D之间,在弦CD上取一点Q,使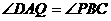 。求证:
。求证: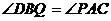
3.
一张纸上画有半径为R的圆O和圆内一定点A,且OA=a,折叠纸片,使圆周上某一点 刚好与A点重合,这样的每一种折法,都留下一条直线折痕,当
刚好与A点重合,这样的每一种折法,都留下一条直线折痕,当 取遍圆周上所有点时,求所有折痕所在直线上点的集合。
取遍圆周上所有点时,求所有折痕所在直线上点的集合。
第二试
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com