
题目列表(包括答案和解析)
2.不等式法:由定义域列出自变量x的不等式,然后用不等式演算法,演算至函数y的不等式,即得
值域。
1.直接法:根据函数的定义域和对应法则,利用学过的基本函数的值域,经过简单的等价变换,直接
求得值域的方法。
3.有实际问题,要由实际意义来确定。
例:求函数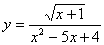 的定义域。
的定义域。
解: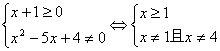
∴函数的定义域是[-1,1]∪(1,4)∪(4,+∞)。
问9.在当前的学习阶段,应该掌握哪些求值域的方法?
[解]应该掌握求值域的下述方法:
2.有抽象问题,要由函数符号的意义来确定;
1.使解析式f(x)有意义;
3.表出定义域,即用{}或区间表示出定义域。
列条件组的法则是:
2.解条件组;
1.列条件组,即列出自变量满足的充要条件;
2.换元法:
第一换元法--凑法
例:已知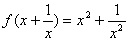 ,求f(x)
,求f(x)
解:把已知等式改写为
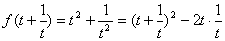 ,
,
即凑成 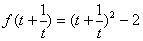
∴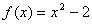
这种换元法叫做凑法。
第二换元法--设法
例:已知f(2x-3)=x,求f(x)。
解:把已知等式改写为
f(2t-3)=t
设2t-3=x,则
∴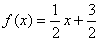
这种换元法叫做设法。
问8.怎样求函数的定义域?
[解]求定义域的一般步骤是:
1.待定系数法(方程组法):设出f(x)的一般式;列出待定系数的方程组;解出待定系数;代回一
般式,得函数解析式f(x),概言为“设、列、解、代”。
例:已知f(x)是一次函数,且2f(x)+f(-x)=3x+1对x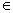 R恒成立,求f(x)。
R恒成立,求f(x)。
解:设f(x)=ax+b (a≠0)(其中a,b为待定系数),则
2(ax+b)+a(-x)+b=3x+1
∵上式对x∈R恒成立,
∴会x=0和x=1,得
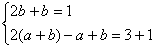
解得 b=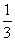 ,a=3
,a=3
∴f(x)=3x+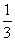
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com