
题目列表(包括答案和解析)
问1:写出映f∶A→B的定义
[解]映射f∶A→B的定义是:设A,B是两个集合,如果按照某种对应法则f,对于集合A中的任何一个元
素,在集合B中都有唯一的元素和它对应,那么这样的对应(包括集合A,B以及A到B的对应法则f)
叫做集合A到集合B的映射,记作f∶A→B。
[评注]这个定义,不要死记硬背,要从以下四点深刻理解它:
1、先记住映射的记号“f∶A→B”,它包括集合A,B以及A到B的对应法则
f(A≠Φ,B≠Φ)。
7.会求一些简单函数的定义域和值域。
6.加深理解函数的概念,理解对应法则的含义,初步掌握函数解析式的两种求法:
(1)待定系数法; (2)换元法
5、掌握分段函数
4、初步掌握函数的三种表示法。
3、掌握函数的要素,能判断两个函数是否为同一个函数。
2、理解函数的概念,正确运用函数记号。
1、了解映射的概念,能判断某些简单的对应是不是映射,在映射基础上加深理解函数。
22.数列{an}满足a1=1,an=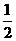 an-1+1 (n≥2)
an-1+1 (n≥2)
⑴ 写出数列{an}的前5项;
⑵ 求数列{an}的通项公式。
21.设数列{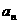 }的首项
}的首项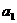 =1前n项和
=1前n项和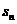 满足关系式
满足关系式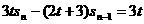 (t>0,n∈N,n≥2).
(t>0,n∈N,n≥2).
(1) 求证数列{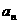 }是等比数列;
}是等比数列;
(2) 设数列{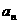 }的公比为
}的公比为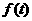 ,作数列{
,作数列{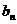 },使
},使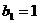 ,
,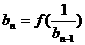 ,(n∈ N,n≥2),求bn.
,(n∈ N,n≥2),求bn.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com