
题目列表(包括答案和解析)
4、方法要灵活
不要把选择题简单地等同于填空题、计算题、证明题。要充分注意用题目提供的信息,灵活运用各种解法,避繁就简,才能事半功倍。
例26、P是边长为2的正方形内切圆圆周上一点,P对正方形两对角线视角分别是 ,则
,则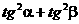 的值
( C )
的值
( C )
(A)2 (B)4 (C)8
(D)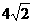
解:抓住特点用特殊值法,可迅速求解。不妨取P点为正方形对角线与它的内切圆的交点,不难求得: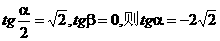 ,代入得
,代入得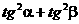 =8
=8
例27、曲线 与直线
与直线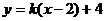 有两交点时,实数
有两交点时,实数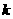 的取值范围
( A )
的取值范围
( A )
(A)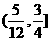 (B)
(B)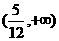 (C)
(C)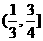 (D)
(D)
解:首先数形结合作出两函数图象,前者为圆心为(0,1)半径为2的上半圆,后者为过定点(2,4)的直线系。如图。有两交点需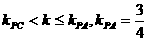 故排除(B)、(D)。那么切线
故排除(B)、(D)。那么切线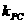 到底是
到底是 ,由选择支中反复出现的
,由选择支中反复出现的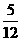 已暗示了答案可能是(A),可进一步代值,由圆心到直线的距离等于半径来验证
已暗示了答案可能是(A),可进一步代值,由圆心到直线的距离等于半径来验证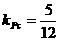 故选(A)
故选(A)
 y
P
C
A
B
O
X y
P
C
A
B
O
X |
例28、梯子10级,一步上一级或2级,规定8步走完有多少种走法 ( B )
(A)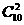 (B)
(B)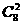 (C)
(C)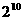 (D)
(D)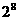
解:设2级需x步,1级y步,有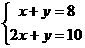 x=2,y=6即10=2
x=2,y=6即10=2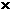 2+6
2+6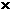 1,进一步研究2步2级的不同位置,故为
1,进一步研究2步2级的不同位置,故为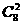 。选(B)
。选(B)
3、分析要全面
分析不全面,有时会使符合题意的解出现重复或遗漏,有时又会让不合题意的解鱼目混珠。
例22、与空间四点等距的平面至少有 ( D )
(A)1个 (B)3个 (C)4个 (D)7个
例48、(97年)四面体的顶点和各棱中点共10个点,在其中取4个不共面的点,不同的取法共有 ( D )
(A)150种 (B)147种 (C)144种 (D)141种
解:本题为近年高考中得分最低的选择题。任取4点有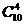 种,其中4点共面的情况有三类。一类:4点位于四面体的同一面内,有
种,其中4点共面的情况有三类。一类:4点位于四面体的同一面内,有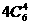 种;二类:中位线构成的平行四边形,有3种;三类:取一棱上3点及对棱的中点,有6种。(最易忽略)故取法有:
种;二类:中位线构成的平行四边形,有3种;三类:取一棱上3点及对棱的中点,有6种。(最易忽略)故取法有: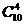 -
-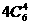 -3-6=141,选(D)
-3-6=141,选(D)
例23、从1~9这九个数字中任取两个不同的数分别作对数的真数和底数,可得不同的对数值有 ( B )
(A)32 (B)53 (C)57 (D)72
例24、若函数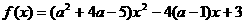 的图象在x轴上方,则实数
的图象在x轴上方,则实数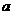 的取值范围 制 ( B )
的取值范围 制 ( B )
(A)(1,19) (B)[1,19) (C)[1,19] (D)以上不对
略析:一定要考虑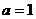 函数退缩为常函数
函数退缩为常函数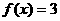 也满足条件,故选(B)
也满足条件,故选(B)
例25、长方体ABCD-A1B1C1D1中,AB=3,BC=2,A1A=1,则从A点出发沿表面到C1的最短距离是 ( C )
(A) (B)
(B)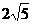 (C)
(C)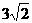 (D)
(D)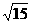
略析:侧面展开要考虑到两种路径再比较大小。选(C)
2、基础要牢靠
选择题小、巧、活的特点。是检查基础知识,考察判断力的好题型。为解题正确而迅速,必须牢固掌握教材中的基础知识。概念不可混淆不清,性质不可似是而非,方法不可模棱两可。
例21、若函数f(x+1)的定义域是[1,2],f(x-2)的定义域是 ( B )
(A)[3,4] (B)[4,5] (C)[2,3] (D)[-2,-3]
分析:对函数定义域及复合函数的意义要充分理解,才不至模棱两可。
解题时,若根据题设推出的结果与选择支都不相同,说明解题有误,须认真检查每个解题环节,找出错误的原因。有时由于概念不清或计算不慎,所得结果与某一干扰支相同,这样陷入“陷阱”。为识破命题者的“陷阱”,提高解选择题的正确率,再强调以下几点:
1、审题要仔细
审题时要逐字逐句推敲,分析隐含条件,掌握关键词句。
例19、已知x1,x2是方程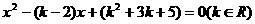 的两实根,则
的两实根,则
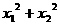 最大值是
( B )
最大值是
( B )
(A)19 (B)18 (C)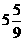 (D)不存在
(D)不存在
分析:由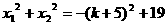 若忽略两实根
若忽略两实根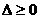 的约束,易错选(A)
的约束,易错选(A)
事实上解出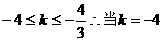 时,最大值为18
时,最大值为18
例20、已知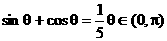 求
求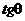 的值
( C )
的值
( C )
(A)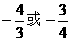 (B)
(B)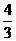 (C)
(C)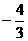 (D)
(D)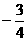
解:若充分注意到题设中的隐含条件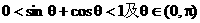 ,可判断
,可判断
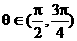 ,从而判定
,从而判定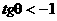 ,可直接选出(C),避免了产生增根错选(A)
,可直接选出(C),避免了产生增根错选(A)
8、逻辑分析
根据提供的选择支结合题意,通过分析确定正确答案。
例17已知集合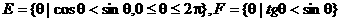 ,那么
,那么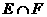 为区间
( A )
为区间
( A )
(A)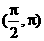 (B)
(B)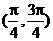 (C)
(C) (D)
(D)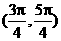
解:(A)(C)排斥,(B)(D)排斥,在(B)中取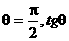 无意义,排除(B),在(D)中取
无意义,排除(B),在(D)中取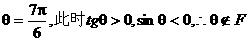 排除(D)同时也排除(C) 故选(A)
排除(D)同时也排除(C) 故选(A)
例18下列四个命题中的假命题是 ( )
A存在无穷多个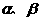 ,使得
,使得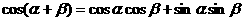
B不存在无穷多个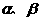 ,使得
,使得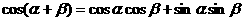
C对任意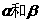 ,使得cos(
,使得cos( )=
)=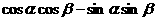
D、不存在这样的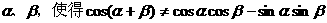
7、逆代验证
例15、(1994年高考文科卷)如果函数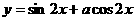 的图象关于直线
的图象关于直线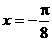 对称,那么
( D )
对称,那么
( D )
(A)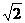 (B)-
(B)-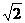 (C)1 (D)-1
(C)1 (D)-1
分析:本题难度系数0.3。许多人在化到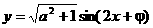 不知如何下手。应注意其对称轴过图象波峰波谷,即最值处。将
不知如何下手。应注意其对称轴过图象波峰波谷,即最值处。将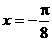 代入有
代入有
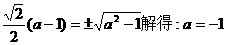 。采用将各值代入验证排除更易推出选(D)
。采用将各值代入验证排除更易推出选(D)
例16若向量m=(2,0),n=(3,0),|a-m|=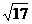 ,|a-n|=4,则向量a为 ( )
A、(-3,±4) B、(4,
±3)
C、(3, ±4) D、(-4,
±3)
,|a-n|=4,则向量a为 ( )
A、(-3,±4) B、(4,
±3)
C、(3, ±4) D、(-4,
±3)
6、结论选择法
由于高考命题原则是“源于教材,而略高于教材”,加上选择题是不必说明理由等特点. 在数学学习过程中可总结出略高于教材的真命题,但又不是课本中的定理、公式,故我们称它们为规律性结论. 利用它可大大简化解题过程,掌握一定量的规律性结论是很有必要的.对于规律性同学们可根据自己的实际情况加以总结.
例14(1998年全国高中数学联赛题)各项都是实数的等比数列{an},前n项的和记为Sn,若S10=10,S30=70,则S40等于()
(A) 150 (B) -200 (C) 150或-200 (D) 400或-50
分析 等比数列{an}的公比为q,前n项和为Sn,则得等比数列又一一求和公式Sm+n=Sm+qmSn.
解法1由“另一求和公式”,得S40=S30+q30S10.
又S30>0,q30>0,S10>0.
∴ S40>0,排除(B)、(C)、(D),而选(A).
解法2由公式,得S30=S20+q20S10=S10+q10S10+q20S10.
从而有q20+q10-6=0,解得q10=2.
∴ S40=S30+q30S10=70+8×10=150,选(A).
5、直观选择法
直观选择法就是通过数形结合的方法,借助图形的直观性,迅速作出判断的一种解题方法.常用的图形有:韦恩图、数轴、三角函数线、函数的图像、方程的曲线、几何图形、表格等.
例13已知α为锐角,且cosα=3/5,cos(α+β)=-5/18,那么β是第( )象限的角
A、一 B、一或二 C、一或三 D、二或三
4、 特征选择法
特征分析选择法是指通过认真地审题,深入挖掘问题的不同特征,将隐含条件、内部结构等显露出来,从而把握住问题脉搏、优化思维,开拓快速解题的捷径.我们可从以下几个方面去分析:条件特征的分析、结论特征的分析、位置特征的分析、结构特征的分析、语言特征的分析等.
例11(1999年全国高考题)若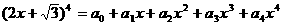 ,则
,则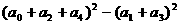 的值为()
的值为()
A. 1 B. 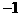 C. 0 D. 2
C. 0 D. 2
解:考察待求式结构
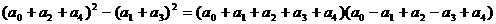
恰是条件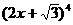 结构中,取特殊值
结构中,取特殊值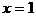 与
与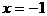 时的积.
时的积.
即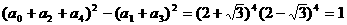 ,故选A
,故选A
说明:纵观问题的条件与结论,某些命题的已知数式结构中常常隐含着某种特殊的关系,通过细致而敏锐的观察,进而联想转化,可实现解题的选择.
例12设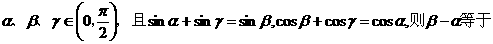
A、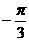 B、
B、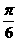 C、
C、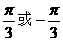 D、
D、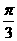 ( )
( )
3、 特例选择法
高考数学选择题是四选一型的单项选择题,对于条件或结论是一般性问题,“特例选择法”是行之有效的方法.此法的主要特征是取特例(如特殊值、特殊函数、特殊角、特殊点、特殊数列等等),进行合理科学的判断--否定或肯定,从而达到快速解题目的.
例8(2002年全国高考题) 不等式(1+x)(1-│x│)>0的解集是( )
(A) {x│0≤x<1} (B) {x│x<0且x≠-1}
(C) {x│-1<x<1} (D) {x│x<1且x≠-1}
分析 本题若用直接法,需分类讨论,计算量大且易出错.而用特殊值法,则能省时又省力.
解:取x=0、-2,显然是原不等式的解,故排除(A)(B)(C),而选(D).
例9若a,b,c成等比数列,m为a、b的等差中项,n为b、c的等差中项,则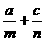 的值为
( )
的值为
( )
A、4 B、3 C、2 D、1
例10(1997年高考试题)不等式组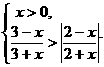 的解集是
( C )
的解集是
( C )
(A)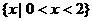 (B)
(B)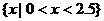
(C)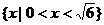 (D)
(D)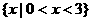
题目设计的四选择支数据:2、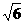 、2.5、3四个数值非常接近。让学生不易取值排除。但聪明的发现将x=
、2.5、3四个数值非常接近。让学生不易取值排除。但聪明的发现将x=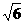 代入能使不等式两边相等为
代入能使不等式两边相等为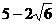 ,考虑不等式解与方程有关,猜答案为(C)
,考虑不等式解与方程有关,猜答案为(C)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com