
题目列表(包括答案和解析)
(17)(本小题12分)
(1)学校开设七门课,每天可排六节课(每门课每天最多排一节),若星期三必须有体育课,但不能排在第一节和第五节,则星期三有多少种不同的排课法?
(2)学校开设七门课,若星期六只能排四节课,但第一节课和第四节课不能排体育课,则星期六共有多少种不同的排课法?
(18)(本小题12分)
在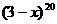 (
(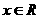 ,
,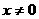 )的展开式中,已知第
)的展开式中,已知第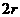 项与第
项与第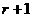 (
(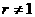 )的二项式系数相等。
)的二项式系数相等。
(1)求 的值;(2)若该展开式的第
的值;(2)若该展开式的第 的值与倒数第
的值与倒数第 项的值的
项的值的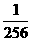 相等,求
相等,求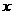 的值。
的值。
(19)(本小题12分)
1994年夏季在美国举行了第15届世界杯足球赛,共有24支队参赛,他们先分成六个小组进行循环赛,决出16强(每队均与本组其他队赛一场,各组一、二名及4支积分较高的第三名晋升16强),这16支队按确定的程序进行淘汰赛,最后决出冠亚军,此外还须决出第三名、第四名,问这次世界杯总共进行了几场比赛?
(20)(本小题12分)
已知 展开式中第6项为21,并且第2项、第3项与第4项系数成等差数列,试求
展开式中第6项为21,并且第2项、第3项与第4项系数成等差数列,试求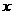 的值。
的值。
(21)(本小题12分)
某工厂为了提高经济效益,充分挖掘生产潜力,现在要利用该厂所有闲置机器协作加工A、B、C、D、E五种产品。为了减轻机器负荷,延长机器的使用寿命,每台机器只允许加工任意两种产品,加工时,任意两种产品中只有一台机器是共用的,且要求加工每种产品所用的机器台数相等。请根据已知条件,求出该厂闲置机器的台数。
(22)(本小题14分)
设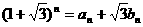 (
(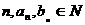 )
)
(1)求证: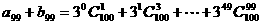
(2)设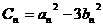 (
( ),求
),求 的值。
的值。
(13)已知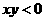 ,且
,且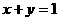 ,而
,而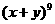 按
按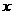 的降幂排列的开展式中,第二项不大于第三项,则
的降幂排列的开展式中,第二项不大于第三项,则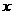 的取值范围是 。
的取值范围是 。
(14)有13名医生,其中女医生6人,男医生7人,现从中抽调5名医生组成医疗小组前往灾区。若医疗小组至少有2名男医生,同时至多有3名女医生,设不同的选派方法种数为 ,则下列等式:①
,则下列等式:① ;②
;②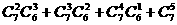 ;③
;③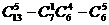 ;④
;④ 。其中能成为
。其中能成为 的算式有
的算式有
(15)在排成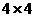 的方阵的16个点中,中心4个点在某一个圆内,其余12个点在圆外,在16个点中任取3个点构成三角形,其中至少有一个顶点在圆风的三角形共有 个。
的方阵的16个点中,中心4个点在某一个圆内,其余12个点在圆外,在16个点中任取3个点构成三角形,其中至少有一个顶点在圆风的三角形共有 个。
(16)关于二项式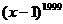 ,有以下四个命题:①该二项开展式中非常数项的系数和是1;②该二项开展中系数最大的项是第1000项;③该二项开展式中第六项为
,有以下四个命题:①该二项开展式中非常数项的系数和是1;②该二项开展中系数最大的项是第1000项;③该二项开展式中第六项为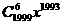 ;④当
;④当 时,
时,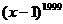 除以2000的余数是1999。其中正确命题的序号是 。(把你认为正确的命题的序号都填上)
除以2000的余数是1999。其中正确命题的序号是 。(把你认为正确的命题的序号都填上)
(1)10名学生相约第二天去春游,本着自愿的原则,规定任何人可选择“去”与“不去,”,则第二天可能出现的不同情况共有的种数为
(A)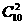 (B)
(B)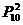 (C)
(C) (D)
(D)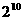
(2)在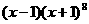 的展开式中,
的展开式中,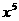 的系数是
的系数是
(A)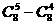 (B)
(B)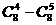 (C)
(C)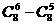 (D)
(D)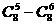
(3)现有6名女学生,分配甲、乙两个宿舍,每个宿舍最多限住4人,则不同的分配方法有
(A)40种 (B)50种 (C)60种 (D)70种
(4)已知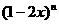 的展开式中,奇数项的二项式系数之和为64,则该二项式开展式的中间项为
的展开式中,奇数项的二项式系数之和为64,则该二项式开展式的中间项为
(A)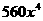 (B)
(B) (C)
(C)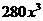 或
或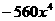 (D)
(D) 或
或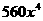
 (5)一杂技团有8名表演魔术或口技的演员,其中6人会演口技,5人会表演魔术,今从这8名演员中选出2人,1 人表演口技,1人表演魔术,则共有选法种数是
(5)一杂技团有8名表演魔术或口技的演员,其中6人会演口技,5人会表演魔术,今从这8名演员中选出2人,1 人表演口技,1人表演魔术,则共有选法种数是
(A)27种 (B)30种 (C)28种 (D)56种
(6)将某城市分为四个区(如图),需要绘制一幅城市分区地图,现有5种不同颜色,图①②③④每区只涂一色,且相邻两区必须涂不同的颜色(不相邻两区所涂颜色不限),则不同的涂色方式有
(A)240种 (B)180种 (C)120种 (D)60种
(7)若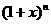 展开式中
展开式中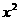 项的系数为
项的系数为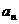 ,则
,则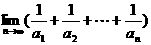 的值是
的值是
(A)1 (B)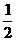 (C)
(C)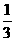 (D)2
(D)2
(8)有“386”、“486”、“586”型电脑各一台,甲、乙、丙、丁四名操作人员的技术等次各不相同,甲、乙会操作三种型号的电脑,而丙不能操作“386”,而丁只会操作“386”,今从四名操作人员中选出3人分别去操作以上电脑,则不同的选派方法有
(A)6种 (B)8种 (C)10种 (D)12种
(9)若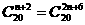 ,且
,且 ,则
,则
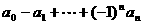 等于
等于
(A)1 (B)16 (C)27 (D)81
(10)教室里六个座位连成一排,安排三名学生就座,每一名学生坐一个座位,恰有两个空位相邻的排法种数是
(A)96 (B)72 (C)48 (D)36
(11)某市学校“减负”后,增加了学生的社会实践活动。该市植物园要在30天内接待20所学校的学生参观,但每天只能安排一所学校,其中有一所学校人数较多,要安排连续参观两天,其余的每所学校只参观一天,则该植物园在这30天中不同的安排方法的种数为
(A)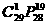 (B)
(B)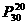 (C)
(C)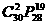 (D)
(D)
(12)二项式 (
( )中系数最大的项是
)中系数最大的项是
(A)第4项 (B)第5项 (C)第4项和第5项 (D)无法确定
12.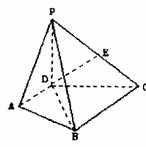 (18分)如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD=DC=1,BC=
(18分)如图,在四棱锥P-ABCD中,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD=DC=1,BC=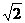
(I) 求PB与平面PDC所成角的大小;
(II) 求二面角D-PB-C的大小;
(III)
若AD= BC,E为PC中点,求证:DE∥平面PAB。
BC,E为PC中点,求证:DE∥平面PAB。
11.(12分)如图,在长方体ABCD-A1B1C1D1中,棱长AB=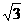 ,AA=1,截面ABC1D1为正方形。
,AA=1,截面ABC1D1为正方形。
(I)
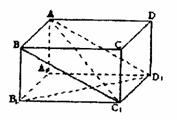 求直线B1D1与平面ABC1D1所成角的大小;
求直线B1D1与平面ABC1D1所成角的大小;
(II) 求二面角B-AC1-B1的大小。
10.如图,直三棱柱ABC-A1B1C1的侧棱和底面边长都是a,截面AB1C与截面A1BC1相交于DE,四面体BB1DE的体积为_________。
9. 已知斜棱柱直截面周长为8,高为4,侧棱与底面成60°角,则斜棱柱侧面积是_________。
已知斜棱柱直截面周长为8,高为4,侧棱与底面成60°角,则斜棱柱侧面积是_________。
8.正方体ABCD-A1B1C1D1中,E、F分别是棱AB、CC1的中点,则异面直线AC与EF所成角的余弦值为________。
7.三棱锥S-ABC中,SA、SB、SC两两垂直,且SA=5,SB=4,SC=3,则SA与BC间的距离等于___________.
6.正三棱锥P-ABC中,E、F是侧棱PB、PC的中点,
若截面AEF垂直于侧面PBC,则棱锥的侧面积与底面积
之比为( )
A.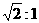 B.
B.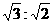 C.
C.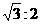 D.
D.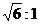
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com