
题目列表(包括答案和解析)
(11)把参数方程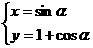 (α是参数)化为变通方程,结果是_____________。
(α是参数)化为变通方程,结果是_____________。
(12) =_____________。
=_____________。
(13)一个圆台的高是上下底面半径的等比中项,这个圆台高为1,母线长为 ,则这个圆台的体积为_____________。
,则这个圆台的体积为_____________。
(14)已知|a+b|<-c(a、b、c∈R),给出下列不等式:
①a<-b-c;②a>-b+c;③a<b-c;④|a|<|b|-c;⑤|a|<|b|-c。
其中一定成立的不等式是:_____________。
(注:把成立的不等式的序号都填上)。
(1)双曲线 的两个焦点坐标分别是()
的两个焦点坐标分别是()
(A) ,
, (B)
(B) ,
,
(C)(-1,0),(1,0)(D)(0,-1),(0,1)
(2)下列四个函数中,在区间(0,1)上为增函数的是()
(A) (B)y=sinx
(B)y=sinx
(C)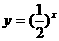 (D)y=arccosx
(D)y=arccosx
(3)如果复数 (其中i为虚数单位,b为实数)的实部和虚部互为相反数,那么b等于()
(其中i为虚数单位,b为实数)的实部和虚部互为相反数,那么b等于()
(A) (B)
(B)
(C) (D)2
(D)2
(4)α,β是两个不重合的平面,在下列条件中,可判定平面α与β平行的是()
(A)m,n是α内两条直线,且m∥β,n∥β
(B)α,β都垂直于平面γ
(C)α内不共线三点到β的距离都相等
(D)m,n是两条异面直线, ,
,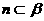 ,且m∥β,n∥α
,且m∥β,n∥α
(5)函数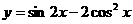 的最大值是()
的最大值是()
(A) (B)
(B)
(C)3(D)2
(6)在等比数列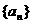 中,
中, ,
, ,则
,则 的值是()
的值是()
(A) (B)
(B)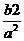
(C) (D)
(D)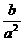
(7)某人制定了一项旅游计划,从7个旅游城市中选择5个进行游览。如果A、B为必选城市,并且在游览过程中必须按先A后B的次序经过A、B两城市(A、B两城市可以不相邻),则有不同的游览线路()
(A)120种(B)240种
(C)480种(D)600种
(8)设偶函数 在(0,+∞)上单调递减,则f(b-2)与f(a+1)的大小关系是()
在(0,+∞)上单调递减,则f(b-2)与f(a+1)的大小关系是()
(A)f(b-2)=f(a+1)(B)f(b-2)>f(a+1)
(C)f(b-2)<f(a+1)(D)不能确定
(9)P是双曲线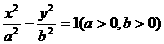 右支上一点,
右支上一点, 、
、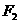 分别是左、右焦点,且焦距为2c,则
分别是左、右焦点,且焦距为2c,则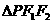 的内切圆圆心的横坐标为()
的内切圆圆心的横坐标为()
(A)a(B)b
(C)c(D)a+b-c
(10)设函数f(x)的定义域为D,如果对于任意的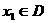 ,存在唯一的
,存在唯一的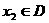 ,使
,使 (C为常数)成立,则称函数y=f(x)在D上的均值为C。给出下列四个函数:
(C为常数)成立,则称函数y=f(x)在D上的均值为C。给出下列四个函数:
① ;②y=4sinx;
;②y=4sinx;
③y=lgx;④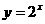
则满足在其定义域上均值为2的所有函数是()
(A)①②(B)③④
(C)①③④(D)①③
22. (本题满分14分)
从一批有5个合格品与3个次品的产品中,一件一件地抽取产品,设各个产品被抽到的可能性相同.记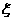 为直到取出的是合格品为止时所需抽取的次数,分别在下列三种情形下求出:
为直到取出的是合格品为止时所需抽取的次数,分别在下列三种情形下求出:
(1) 每次抽取的产品都不放回到这批产品中的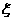 的分布列和所需平均抽取的次数;
的分布列和所需平均抽取的次数;
(2) 每次抽取的产品都立即放回到这批产品中,然后再抽取一件产品的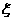 的分布列;
的分布列;
(3) 每次抽取一件产品后,总将一件合格品放入这批产品中的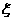 的分布列.
的分布列.
21. (本题满分12分)
已知测量误差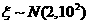 (单位:㎝ ),
(单位:㎝ ), .
.
(1) 求一次测量中误差的绝对值不超过8 ㎝ 的概率;
(2) 必须进行多少次测量才能使至少有一次测量的误差的绝对值不超过8 ㎝ 的概率大于 0.9 ?
20. (本题满分12分)
若随机事件A在一次试验中发生的概率为P ( 0<P<1 ),用随机变量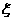 表示A在一次试验中发生的次数. (1) 求方差
表示A在一次试验中发生的次数. (1) 求方差 的最大值;
的最大值;
(2) 求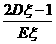 的最大值.
的最大值.
19. (本题满分12分)
甲、乙两名射手在一次射击中的得分是两个随机变量,分别记为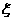 和
和 ,它们的分布列分别为
,它们的分布列分别为
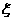 |
0 |
1 |
2 |
|
P |
0.1 |
a |
0.4 |
 |
0 |
1 |
2 |
|
P |
0.2 |
0.2 |
b |
(1) 求a , b 的值
(2) 计算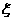 和
和 的期望与方差,并以此分析甲、乙两射手的技术情况.
的期望与方差,并以此分析甲、乙两射手的技术情况.
18. (本题满分12分)
已知随机变量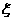 的分布列为
的分布列为
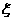 |
1 |
2 |
3 |
|
P |
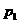 |
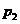 |
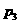 |
且已知  , 求: (1)
, 求: (1) 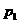 ,
,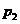 ,
,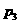
(2) 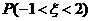 ,
, 
17. (本题满分12分)
假定每人生日在各个月份的机会都是相等的,
求: (1) 某班的60个人中生日在一月份的平均人数;
(2) 该班的60个人中有2人生日在第一季度的概率(只列出式子即可)
16. 设随机变量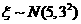 ,则可知
,则可知 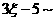 _________________
_________________
15. 有一个简单的随机样本: 10, 12, 9, 14, 13
则样本平均数 =__________ ,样本方差
=__________ ,样本方差 =___________
=___________
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com