
题目列表(包括答案和解析)
1、已知集合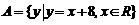 ,
,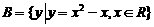 ,则
,则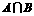 为( )
为( )
A、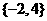 B、
B、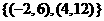 C、
C、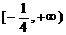 D、R
D、R
22.(本小题满分14分)
已知一列非零向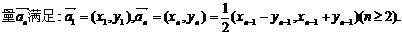
(Ⅰ)证明: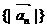 是等比数列;
是等比数列;
(Ⅱ)求向量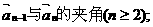
(Ⅲ)设 一列,记为
一列,记为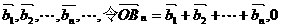 为坐标原点,求点列{Bn}的极限点B的坐标.
为坐标原点,求点列{Bn}的极限点B的坐标.
(注:若点Bn坐标为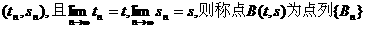 的极限点.)
的极限点.)
21.(本小题满分12分)
如图,已知在坐标平面内,M、N是x轴上关于原点O对称的两点,P是上半平面内一点,△PMN的面积为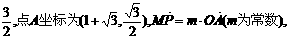
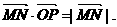
(Ⅰ)求以M、N为焦点且过点P的椭圆方程;
(Ⅱ)过点B(-1,0)的直线l交椭圆于C、D两点,交直线x=-4于点E,点B、E分
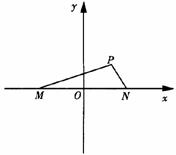
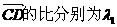 、
、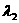 ,求证:
,求证: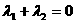 .
.
20.(本小题满分12分)
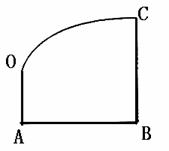 某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地规划建成一个矩形高科技工业园区.已知AB⊥BC,OA//BC,且AB=BC=2AO=4km,曲线段OC是以点O为顶点且开口向右的抛物线的一段.如果要使矩形的相邻两边分别落在AB、BC上,且一个顶点落在曲线段OC上,问应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到0.1km2).
某地政府为科技兴市,欲将如图所示的一块不规则的非农业用地规划建成一个矩形高科技工业园区.已知AB⊥BC,OA//BC,且AB=BC=2AO=4km,曲线段OC是以点O为顶点且开口向右的抛物线的一段.如果要使矩形的相邻两边分别落在AB、BC上,且一个顶点落在曲线段OC上,问应如何规划才能使矩形工业园区的用地面积最大?并求出最大的用地面积(精确到0.1km2).
19.(本小题满分12分)
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为正方形,PD=DC,E、F分别是AB、PB的中点.
(Ⅰ)求证:EF⊥CD;
(Ⅱ)在平面PAD内求一点G,使GF⊥平面PCB,并证明你的结论;
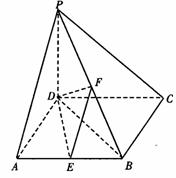 (Ⅲ)求DB与平面DEF所成角的大小.
(Ⅲ)求DB与平面DEF所成角的大小.
18.(本小题满分12分)
抛掷两个骰子,当至少有一个2点或3点出现时,就说这次试验成功.
(Ⅰ)求一次试验中成功的概率;
(Ⅱ)求在4次试验中成功次数ξ的概率分布列及ξ的数学期望与方差.
17.(本小题满分12分)
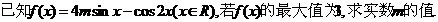
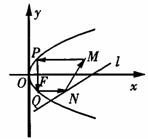
16.如图,从点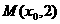 发出的光线沿平行于抛物线
发出的光线沿平行于抛物线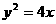 的轴的方向射向此抛物线上的点P,反射后经焦点F又射向抛物线上的点Q,再反射后沿平行于抛物线的轴的方向射向直线
的轴的方向射向此抛物线上的点P,反射后经焦点F又射向抛物线上的点Q,再反射后沿平行于抛物线的轴的方向射向直线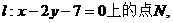 再反射后又射回点M,则
再反射后又射回点M,则
x0= .
14.如图,一艘船上午9:30在A处测得灯塔S在它的北偏东30°处,之后它继续沿正北方向匀速航行,上午10:00到达B处,此时又测得灯塔S在它的北偏东75°处,且与它相距8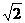 n mile.此船的航速是
n mile/h.
n mile.此船的航速是
n mile/h.
 15.若不等式
15.若不等式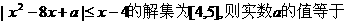 .
.
13. 展开式中的常数项为
.
展开式中的常数项为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com