
题目列表(包括答案和解析)
(17)(本小题满分10分)
已知随机变量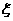 的分布列为
的分布列为
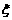 |
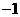 |
0 |
1 |
2 |
3 |
|
P |
0.3 |
0.1 |
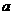 |
0.3 |
0.2 |
求实数a的值,并求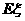 和
和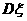 .
.
(18)(本小题满分12分)
已知函数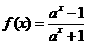
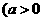 ,
,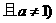 .
.
(Ⅰ)求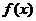 的反函数
的反函数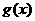 ;
;
(Ⅱ)若函数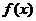 过点
过点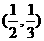 ,则函数
,则函数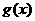 过点
过点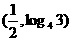 吗?为什么?
吗?为什么?
(19)(本小题满分12分)
已知正三棱柱ABC-A1B1C1,底面边长AB=2,AB1⊥BC1,点O、O1分别是
 边AC、A1C1的中点,建立如图所示的空间直角坐标系.
边AC、A1C1的中点,建立如图所示的空间直角坐标系.
(Ⅰ)求正三棱柱ABC-A1B1C1的侧棱长;
(Ⅱ)求异面直线AB1与BC所成角的大小.
(20)(本小题满分12分)
如图,有甲乙两个村庄,甲村位于一直线河岸的岸边A处,乙村与甲村在河的同侧,乙村位于离河岸40km的B处,乙村到河岸的垂足D与A相距50km,两村要在此岸边合建一个自来水厂C,从自来水厂到甲村和乙村的水管费用分别为每千米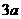 元和
元和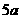 元. 现要进行工程费用测算.
元. 现要进行工程费用测算.
(Ⅰ)求出水管总费用关于水厂C到D的距离的函数
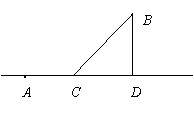 关系式;
关系式;
(Ⅱ)问自来水厂C建在何处,才能使水管总费用最
省?
(21)(本小题满分14分)
在以O为原点的直角坐标系中,点A(3,-1)为 的直角顶点. 已知|AB|=2|OA|,且点B的纵坐标大于零.
的直角顶点. 已知|AB|=2|OA|,且点B的纵坐标大于零.
(Ⅰ)求向量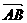 的坐标;
的坐标;
(Ⅱ)是否存在实数a,使二次函数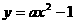 的图像上总有关于直线OB对称的两个不同的点?若不存在,说明理由;若存在,求a的取值范围.
的图像上总有关于直线OB对称的两个不同的点?若不存在,说明理由;若存在,求a的取值范围.
(22)(本小题满分14分)
若数列{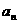 }的通项
}的通项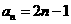 ,设数列{
,设数列{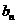 }的通项
}的通项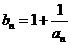 ,又记
,又记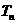 是数列{
是数列{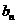 }
}
的前n项的积.
(Ⅰ)求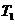 ,
,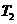 ,
,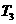 的值;
的值;
(Ⅱ)试比较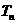 与
与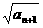 的大小,并证明你的结论.
的大小,并证明你的结论.
(13)若复数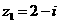 ,
,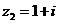 ,则
,则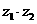 的模为__________.
的模为__________.
(14)若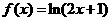 ,则
,则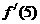 =
.
=
.
(15)已知函数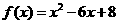
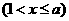 ,并且函数
,并且函数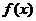 的最小值为
的最小值为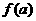 ,则实数
,则实数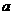 的取值范围是
.
的取值范围是
.
(16)在某次花样滑冰比赛中,发生裁判受贿事件,竞赛委员会决定将裁判由原来的9名增至14名,但只任取其中7名裁判的评分作为有效分. 若14名裁判中有2人受贿,则有效分中没有受贿裁判的评分的概率是 (结果用数值表示).
一项是符合题目要求的.
(1)集合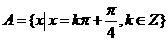 ,
,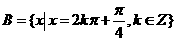 ,则有
,则有
(A)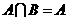 (B)
(B)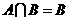 (C)
(C)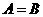 (D)
(D)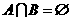
(2)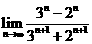 等于
等于
(A)0
(B)1 (C)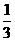 (D)
(D)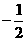
(3)某单位有职工160人,其中业务人员120人,管理人员16人,后勤人员24人. 为了
了解职工的某种情况,要从中抽取一个容量为20的样本. 若要用分层抽样的方法,则抽
取的业务人员,管理人员,后勤人员的人数分别为
(A)7、6、7 (B)15、2、3 (C)10、4、6 (D)17、1、2
(4)已知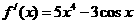 ,
, ,则
,则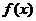 等于
等于
(A)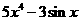 (B)
(B)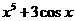 (C)
(C)
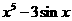 (D)
(D) 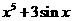
(5)复数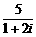 的共轭复数是
的共轭复数是
(A)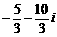 (B)
(B)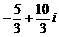 (C)
(C)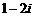 (D)
(D)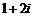
(6)已知命题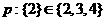 ,命题
,命题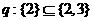 ,有如下判断:①
,有如下判断:①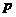 或
或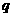 为真;②
为真;② 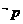 或
或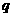 为假;③
为假;③ 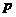 且
且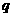 为真;④
为真;④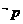 为真.其中正确的是
为真.其中正确的是
(A)①② (B)①④ (C)②④ (D)③④
(7)给定两个向量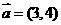 ,
,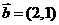 ,
,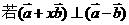 ,则x的值等于
,则x的值等于
(A)-3
(B)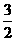 (C)3 (D)-
(C)3 (D)-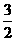
(8)已知函数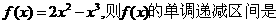
(A)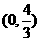 (B)
(B)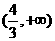 (C)
(C)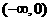 (D)
(D)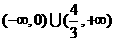
(9)设函数f ( x ) 是定义域为R且周期为3的奇函数,若 f ( 1 ) =1 ,f ( 2 ) = a ,则
(A) a =1 (B) a = -1 (C) a = 2 (D) a= -2
(10)从甲地到乙地通话m分钟的电话费由函数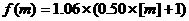 给出,其中m>0, [m]表示大于或等于m的最小整数,如:[3]=3,[3.1]=4, [3.7]=4,则从甲地到乙地通话时间为5.5分钟的电话费为
给出,其中m>0, [m]表示大于或等于m的最小整数,如:[3]=3,[3.1]=4, [3.7]=4,则从甲地到乙地通话时间为5.5分钟的电话费为
(A)3.71元 (B)3.97元 (C) 4.71元 (D) 4.24元
(11)设A、B、C、D是空间不共面的四点,且满足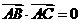 ,
,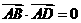 ,
,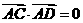 则△BCD是
则△BCD是
(A) 锐角三角形 (B) 直角三角形
(C) 钝角三角形 (D) 以上都有可能
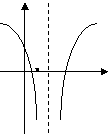
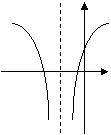 (12)函数
(12)函数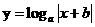 (
(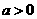 ,
,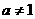 ,
,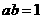 )的图象可能是
)的图象可能是
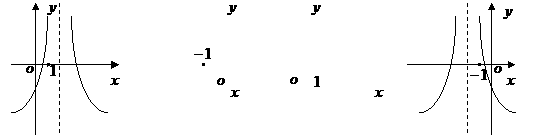 (A)
(B)
(C)
(D)
(A)
(B)
(C)
(D)
第Ⅱ卷(非选择题 共90分)
第Ⅱ卷全部是非选择题,必须在答题区域内,用黑色字迹的钢笔或签字笔作答,不能答在试卷上,否则答案无效.
22.(本小题满分14分)
对于函数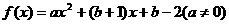 ,若存在实数
,若存在实数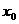 ,使
,使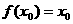 成立,则称
成立,则称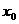 为
为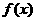 的不动点.
的不动点.
(1)当a=2,b=-2时,求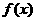 的不动点;
的不动点;
(2)若对于任何实数b,函数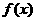 恒有两相异的不动点,求实数a的取值范围;
恒有两相异的不动点,求实数a的取值范围;
(3)在(2)的条件下,若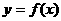 的图象上A、B两点的横坐标是函数
的图象上A、B两点的横坐标是函数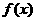 的不动点,
的不动点,
且直线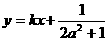 是线段AB的垂直平分线,求实数b的取值范围.
是线段AB的垂直平分线,求实数b的取值范围.
[机密★启用前]
21.(本小题满分12分)
已知点H(-6,0),点P在y轴上,点Q在x轴的正半轴上,点M在直线PQ上,且满足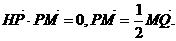
(1)当点P在y轴上移动时,求点M的轨迹C;
(2)过点T(-2,0)作直线l与轨迹C交于A、B两点,若在x轴上存在一点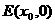 ,
,
使得△AEB是以点E为直角顶点的直角三角形,求直线l的斜率k的取值范围.
20.(本小题满分12分)
设数列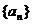 是等比数列,
是等比数列,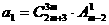 ,公比q是
,公比q是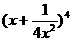 的展开式中的第二项
的展开式中的第二项
(按x的降幂排列).
(1)用n,x表示通项an与前n项和Sn;
(2)若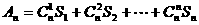 ,用n,x表示An.
,用n,x表示An.
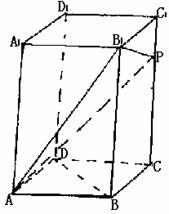
19.(本小题满分12分)
在正四棱柱ABCD-A1B1C1D1中,侧棱是底面边长的2倍,P是侧棱CC1上的任一点.
(1)求证:不论P在侧棱CC1上何位置,总有BD⊥AP;
(2)若CC1=3C1P,求平面AB1P与平面ABCD所成二面角的余弦值;
(3)当P点在侧棱CC1上何处时,AP在平面B1AC上的射影是∠B1AC的平分线.
18.(本小题满分12分)
为了测试甲、乙两名射击运动员的射击水平,让他们各向目标靶射出10次,其中甲击中目标7次,乙击中目标6次,若再让甲、乙两人各自向目标靶射击3次,求:
(1)甲运动员恰好击中目标2次的概率是多少?
(2)两名运动员都恰好击中目标2次的概率是多少?(结果保留两个有效数字).
17.(本小题满分12分)
△ABC中,三个内角分别是A、B、C,向量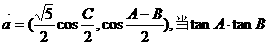
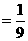 时,求
时,求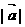 .
.
16.过双曲线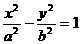 的右焦点F(c,0)的直线交双曲线于M、N两点,交y轴于P
的右焦点F(c,0)的直线交双曲线于M、N两点,交y轴于P
点,则有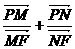 的定值为
的定值为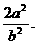 类比双曲线这一结论,在椭圆
类比双曲线这一结论,在椭圆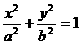 (a>b
(a>b
>0)中,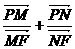 是定值
.
是定值
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com