
题目列表(包括答案和解析)
21、(本小题满分12分)
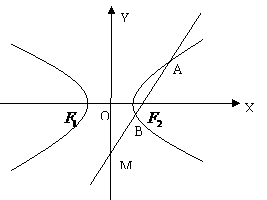
如图:双曲线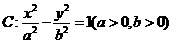 的两个焦点分别为
的两个焦点分别为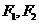 ,斜率为
,斜率为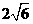 的直线
的直线 过焦点
过焦点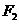 与双曲线交于
与双曲线交于 两点,与
两点,与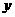 轴交于点
轴交于点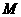 ,若
,若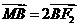 。
。
(1)求双曲线离心率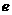 的值;
的值;
(2)若弦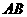 的中点到右准线的距离为
的中点到右准线的距离为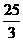 时,求双曲线的方程。
时,求双曲线的方程。
20、(本小题满分12分)
已知函数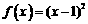 ,数列
,数列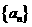 是公差为
是公差为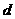 的等差数列,
的等差数列,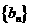 是公比为
是公比为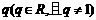 的等比数列,若
的等比数列,若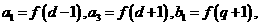
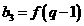 。
。
(1)求数列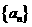 和
和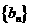 的通项公式;
的通项公式;
(2)设数列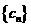 的前
的前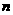 项和
项和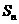 为,且对一切自然数
为,且对一切自然数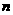 均有:
均有: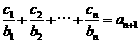 成立,求
成立,求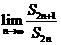 。
。
19、(本小题满分12分)
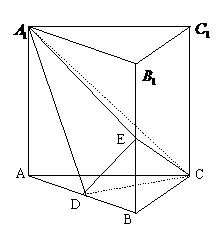 如图,直三棱柱
如图,直三棱柱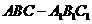 中,
中, 为
为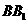 中点,
中点,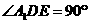
(1)求证:
(2)求二面角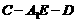 的大小;
的大小;
(3)求三棱锥 的体积。
的体积。
18、(本小题满分12分)
一名学生骑自行车上学,从他的家到学校的途中有6个交通岗,假设他在各交通岗遇到红灯的事件是独立的,并且概率都是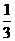
(1)求这名学生首次遇到红灯前,已经过了两个交通岗的概率;
(2)求这名学生在途中遇到红灯数 的期望与方差。
的期望与方差。
解:(1)当这名学生首次遇到红灯前,已经过了两个交通岗的,则必须是这个学生通过第一个交通岗和第二个交通岗都遇到绿灯,且通过第三次交通岗时是红灯,遇到绿灯的概率是1-1/3=2/3,且它们彼此之间互相独立,
所以所求的概率是P=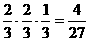
答………
(2)途中遇到红灯数满足 ~B(6,1/3)期望E
~B(6,1/3)期望E =6*1/3=2
=6*1/3=2
方差D =6*1/3*2/3=4/3
=6*1/3*2/3=4/3
答…
17、(本小题满分12分)
已知: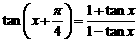 ,且
,且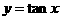 的最小正周期
的最小正周期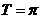 。若
。若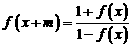 对于正的常数
对于正的常数 和任意实数
和任意实数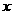 都成立,判断
都成立,判断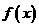 是否是周期函数?如果是,猜测是多少,并加以证明。
是否是周期函数?如果是,猜测是多少,并加以证明。
解:f(x)是周期函数,其周期是4m,下面给出具体的证明。

16、设函数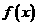 和下面的7个论断:
和下面的7个论断:
①在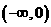 上
上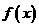 是增函数; ②
是增函数; ②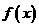 有最大值1;
有最大值1;
③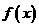 有最小值0;
④
有最小值0;
④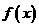 的图象过
的图象过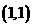 点;
点;
⑤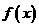 的图象过
的图象过 点; ⑥在
点; ⑥在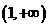 上
上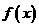 为增函数;
为增函数;
⑦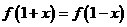 。
。
写出一个函数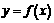 的解析式,使它满足上面的7个论断中的4个论断即可,
的解析式,使它满足上面的7个论断中的4个论断即可, 1-|x-1|.
1-|x-1|.
15、已知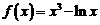 ,则
,则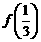 与
与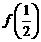 的大小关系是f(1/3)>f(1/2).
的大小关系是f(1/3)>f(1/2).
14、已知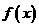 是定义在
是定义在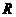 上的奇函数,它的最小正周期是3,则
上的奇函数,它的最小正周期是3,则 0.
0.
13、设数列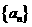 满足
满足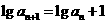 ,且
,且 ,则
,则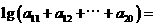 11 .
11 .
12、甲烷分子由一个碳原子和四个氢原子组成,其空间构型为一个正四面体,碳原子位于正四面体的中心,四个氢原子分别位于该四面体的四个顶点上。若将碳原子和氢原子均视为一个点(体积忽略不计),且已知氢原子间的距离为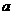 ,则碳原子和氢原子间的距离为( D )
,则碳原子和氢原子间的距离为( D )
A.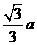 ;
B.
;
B.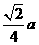 ; C.
; C.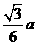 ;
D.
;
D.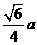
第Ⅱ卷(非选择题)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com