
题目列表(包括答案和解析)
3.双曲线kx2+5y2=5的一个焦点是(0,2),则k等于( )
A.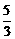 B.-
B.-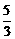 C.
C.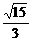 D.-
D.-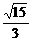
2、抛物线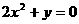 的焦点坐标是 ( )
的焦点坐标是 ( )
A.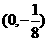 B.
B.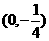 C.
C.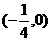 D.
D.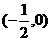
1.已知log2a,log2b,2成等差数列,则M(a,b)的轨迹为 ( )
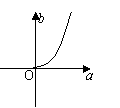
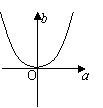
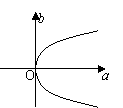
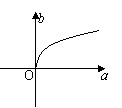
(A) (B) (C) (D)
21.(本小题满分12分)已知函数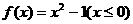 ,数列
,数列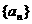 满足
满足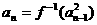
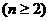 且
且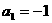 ;
;
(1)求数列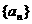 的通项公式;
的通项公式;
(2)若数列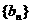 的通项
的通项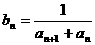 ,
,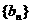 的前
的前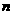 项之和为
项之和为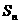 ,试比较
,试比较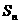 和
和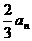 的大小. 21.(12分)(1)解:由
的大小. 21.(12分)(1)解:由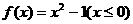 ,得
,得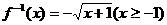 ,
,
又
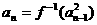
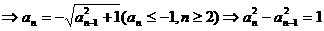 ,
,
所以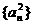 是首项
是首项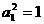 ,公差为1的等差数列,故
,公差为1的等差数列,故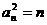 即
即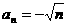 。
。
(2)由(1)得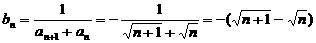 ,所以
,所以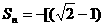
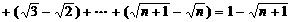 ,令
,令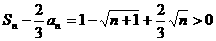
解得: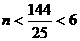 ,所以当
,所以当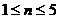 时,
时,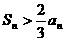 ;当
;当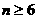 时,
时, 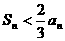 。
。
22.(1)设{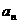 ,
,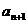 }的公比为q(
}的公比为q(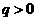 )且
)且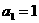 ,
,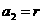 (
( ),由不等式
),由不等式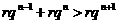
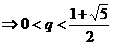 (2)∵
(2)∵ 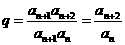 (
(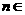 N),
N),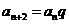 .又
.又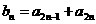 ,∴
,∴ 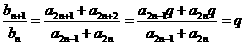 .又
.又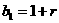
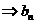 =(1+r)
=(1+r)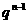 ,
,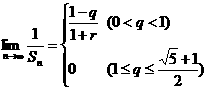
(3)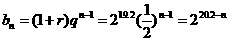 .∴
.∴ 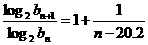 .设
.设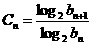 ,则①当
,则①当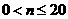 时,
时,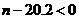 .∴ 当
.∴ 当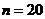 时,
时, 最小(
最小(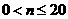 ),
),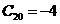 ;②当
;②当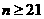 时,
时,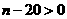 ,当
,当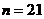 时,
时, 最大(
最大(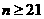 ).
).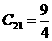
21.(I)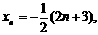
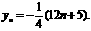 ∴点Pn坐标为
∴点Pn坐标为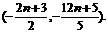
(II)设Cn方程为: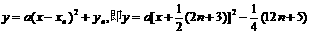 ,①
,①
把Dn(0,n2+1)代入①式得:a=1,∴Cn方程为: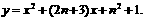
过点Dn且斜率为kn的直线ln 的方程为: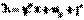
把ln代入Cn得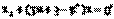 ,∴ln与Cn只有一个交点 ∴△=0,即kn=2n+3.
,∴ln与Cn只有一个交点 ∴△=0,即kn=2n+3.

(III)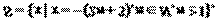
T=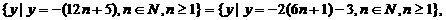
∴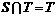 . T中最大数为a1=-17,设{an}的公差为d,则
. T中最大数为a1=-17,设{an}的公差为d,则
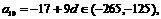 由此得:
由此得: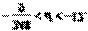
又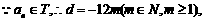
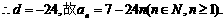
20.设月利率为r,每月还款数为a元,总贷款数为A元,还款期限为n月.
第1月末欠款数 A(1+r)-a,
第2月末欠款数 [A(1+r)-a](1+r)-a= A(1+r)2-a (1+r)-a,
第3月末欠款数 [A(1+r)2-a (1+r)-a](1+r)-a =A(1+r)3-a (1+r)2-a(1+r)-a,
……
第n月末欠款数 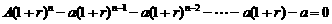 ,
,
得: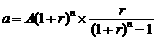 .
.
(I) 对于12年期的10万元贷款,n=144,r=4.455‰,
∴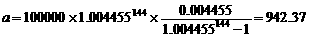 ,
,
对于15年期的15万元贷款,n=180,r=5.025‰,
∴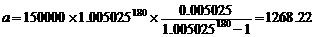 .由此可知,汪先生家前12年每月还款942.37+1268.22=2210.59元,后3年每月还款1268.22元.
.由此可知,汪先生家前12年每月还款942.37+1268.22=2210.59元,后3年每月还款1268.22元.
(II) 至12年末,汪先生家按计划还款以后还欠商业贷款
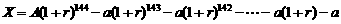 .
.
其中A=150000,a=1268.22,r=5.025‰ , ∴X=41669.53.
再加上当月的计划还款数2210.59元,当月共还款43880.12元.
19. Ⅰ.当n=1时,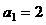 .
Ⅱ.当
.
Ⅱ.当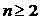 时,
时,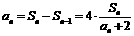
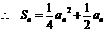
当n=1时,也符合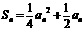
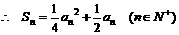
Ⅲ. 当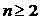 时,
时,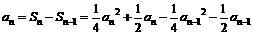
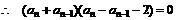
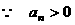 ,
, 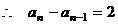
于是数列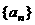 是首项为2,公差为2的等差数列.
是首项为2,公差为2的等差数列.
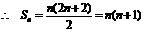 ,
, 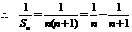 ,
, 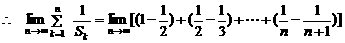
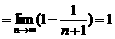 .
.
18.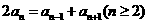
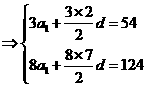
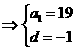
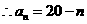 ………..3
………..3
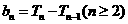
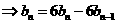
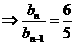
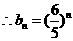 …………………….6
…………………….6
(2) 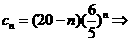
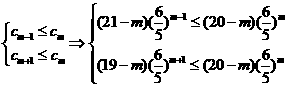
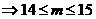 ………………………………………………………….12
………………………………………………………….12
17、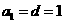 , ,
, , 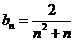 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com