
题目列表(包括答案和解析)
6、已知正四棱锥以棱长为1的正方体的某个面为底面,且与该正方体有相同的全面积,则这一正四棱锥的侧棱与底面所成的角的余弦值为( )
A 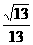 B
B 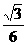 C
C 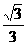 D
D 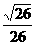
5、已知椭圆的左、右焦点分别是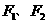 ,以
,以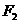 为圆心作圆经过椭圆中心,且与椭圆相交于M点,直线
为圆心作圆经过椭圆中心,且与椭圆相交于M点,直线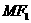 与圆相切,则该椭圆的离心率e=(
)
与圆相切,则该椭圆的离心率e=(
)
A 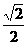 B
B 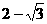 C
C
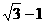 D
D 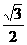
4、已知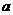 、b为不相等的两个正数,若A是
、b为不相等的两个正数,若A是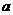 、b的等差中项,正数G是
、b的等差中项,正数G是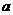 、b的等比中项,则( )
、b的等比中项,则( )
A 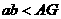 B
B 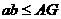 C
C 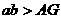 D
D
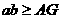
3、已知钝角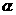 的终边经过点
的终边经过点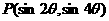 ,且
,且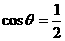 ,则
,则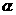 为( )
为( )
A 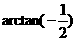 B
B  C
C  D
D 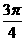
2、下列命题正确的是( )
A 若A(-2,4), B(2,1)则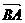 与x轴正方向的夹角为
与x轴正方向的夹角为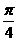 B
B
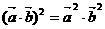
C 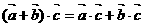 D 若
D 若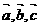 为非零向量,且
为非零向量,且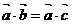 则
则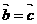
1、 已知集合M=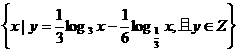 ,若
,若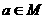 ,则
,则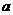 的值可以是( )
的值可以是( )
A
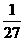 B
B 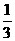 C 3
D 9
C 3
D 9
22.(本小题满分14分)
对于函数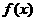 ,若存在
,若存在 成立,则称
成立,则称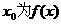 的不动点。如果函数
的不动点。如果函数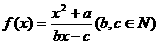 有且只有两个不动点0,2,且
有且只有两个不动点0,2,且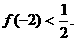
(I)求函数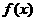 的解析式;
的解析式;
(II)已知各项不为零的数列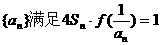 ,求数列通项
,求数列通项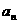 ;
;
(III)如果数列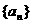 满足
满足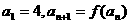 ,求证:当
,求证:当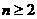 时,恒有
时,恒有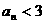 成立.
成立.
高中学生学科素质训练
21.(本小题满分14分)
设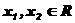 ,常数
,常数 ,定义运算“
,定义运算“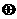 :
: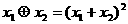 ”;“ :
”;“ :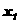
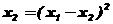 ”
”
 (I)若
(I)若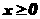 ,求动点
,求动点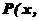 [(
[(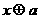 )
)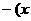
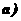 ]1/2)的轨迹C的方程;
]1/2)的轨迹C的方程;
(II)已知直线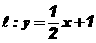 与(1)中的轨迹C交于
与(1)中的轨迹C交于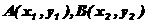 两点,
两点,

 若[(
若[(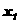
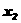 )+(
)+(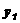
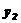 )]1/2=
)]1/2= ,试求
,试求 的值;
的值;
 (III)设
(III)设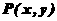 是平面上任意一点,定义
是平面上任意一点,定义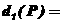 {
{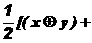
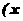
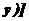 }1/2,
}1/2,

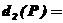 [
[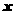
 ]1/2,在轨迹C上是否存在两点
]1/2,在轨迹C上是否存在两点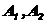 ,使其满足
,使其满足 ,
,
若存在,请求出 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
20.(本小题满分12分)
在一很大的湖岸边(可视湖岸为直线)停放着一只小船,由于缆绳突然断开,小船被风刮跑,其方向与湖岸成15°角,速度为2.5km/h,同时岸边有一人,从同一地点开始追赶小船,已知他在岸上跑的速度为4km/h,在水中游的速度为2km/h.,问此人能否追上小船.若小船速度改变,则小船能被人追上的最大速度是多少?
19.(本小题满分12分)
某银行准备新设一种定期存款业务,经预测存款量与利率的平方成正比,比例系数为k(k>0),贷款的利率为4.8%。又银行吸收的存款能全部放贷出去。
(I)若存款的利率为x,x∈(0,0.048),试写出存款量g(x)及银行支付给储户的利息h(x);
 (II)存款利率定为多少时,银行可获得最大利益?
(II)存款利率定为多少时,银行可获得最大利益?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com