
题目列表(包括答案和解析)
1.设f(x)=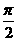 +arctgx,f(x)的反函数是f-1(x),则f-1(
+arctgx,f(x)的反函数是f-1(x),则f-1(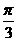 )等于
)等于
A.-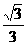 B.-
B.-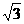 C.
C. 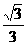 D.
D.
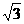
(19)(本小题满分12分)
在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c,且a、b、3c成等比数列,又
∠A-∠C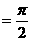 .
试求∠A、∠B、∠C的值.
.
试求∠A、∠B、∠C的值.
(20)(本小题满分10分)
理科作:已知两个复数集合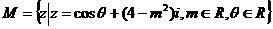 ,
,
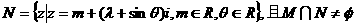 ,求实数λ的取值范围.
,求实数λ的取值范围.
文科作:设函数f(x)的定义域为R,且在其定义域R上,总有f(x)=–f(x+2),又当
–1<x≤1时,f(x)=x2+2x.
(Ⅰ)求当3<x≤5是, 函数f(x)的解析式.
(Ⅱ)试判断函数f(x)在(3,5]上的增减性,并予以证明.
 (21)(本小题满分14分)
(21)(本小题满分14分)
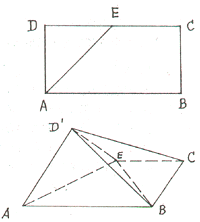
如图:矩形ABCD,AB=2AD=2a,E是CD边的中点,
以AE为棱,将△DAE向上折起,将D变到D'的位置,
使面D'AE与面ABCE成直二面角.
(Ⅰ)求直线D'B与平面ABCE所成的角的正切值;
(Ⅱ)求证:AD'⊥BE;
(Ⅲ)求四棱锥D'-ABCE的体积;
(Ⅳ)求异面直线AD'与BC所成的角.
(文科学生只作(Ⅰ)、(Ⅱ)、(Ⅲ))
(22)(本小题满分12分)
无穷等比数列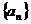 的首项a1=1,其公比q为实常数,且
的首项a1=1,其公比q为实常数,且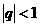 ,数列
,数列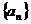 的前n项和为Sn且其各项和为S,数列
的前n项和为Sn且其各项和为S,数列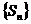 的前n项和为Tn.
的前n项和为Tn.
(Ⅰ)求Tn.(将Tn写成关于q的表达式)
(Ⅱ)求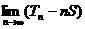 .(写成关于q的表达式)
.(写成关于q的表达式)
(23)(本小题满分12分)
某隧道长a米,最高限速为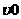 米/秒,一个匀速行进的车队有10辆车,每辆车长为l米,相邻两车之间距离m(米)与车速υ(米/秒)的平方成正比,比例系数为k,自第1辆车车头进隧道至第10辆车车尾离开隧道时所用的时间为t秒.
米/秒,一个匀速行进的车队有10辆车,每辆车长为l米,相邻两车之间距离m(米)与车速υ(米/秒)的平方成正比,比例系数为k,自第1辆车车头进隧道至第10辆车车尾离开隧道时所用的时间为t秒.
(Ⅰ)求出函数t=f(υ)的解析式,并求定义域;
(Ⅱ)求车队通过隧道时间t的最小值,并求出t取得最小值时υ的大小.
(24)(本小题满分14分)
设正方形ABCD的外接圆方程为x2+y2–6x+a=0(a<9),C、D点所在直线l的斜率为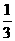 .
.
(Ⅰ)求外接圆圆心M点的坐标及正方形对角线AC、BD的斜率;
(Ⅱ)理科作:如果在x轴上方的A、B两点在一条以原点为顶点,以x轴为对称轴的抛物线上,求此抛物线的方程及直线l的方程.
文科作:如果ABCD的外接圆半径为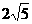 ,在x轴上方的A、B两点在一条以x轴为对称轴的抛物线上,求此抛物线的方程及直线l的方程.
,在x轴上方的A、B两点在一条以x轴为对称轴的抛物线上,求此抛物线的方程及直线l的方程.
(15)设等差数列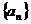 共有3n项,它的前2n项之和是100,后2n项之和是200,则该等差数列的中间n项之和等于
.
共有3n项,它的前2n项之和是100,后2n项之和是200,则该等差数列的中间n项之和等于
.
(16)以椭圆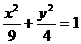 的中心O为顶点,以椭圆的左准线
的中心O为顶点,以椭圆的左准线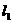 为准线的抛物线与椭圆的右准线
为准线的抛物线与椭圆的右准线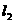 交于A、B两点,则
交于A、B两点,则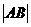 的值为 .
的值为 .
(17)若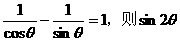 的值等于
.
的值等于
.
(18)人造地球同步通讯卫星的运行轨道是圆,卫星距地面高度是19200km地球半径取6400km,若电磁波是直线传播,那么卫星覆盖的地球表面区别(是一个球冠)的面积与地球表面积之比是 .
(1)sin15°cos165°的值等于 ( )
(A)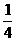 (B)
(B)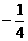 (C)
(C)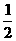 (D)
(D)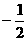
(2)双曲线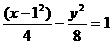 的渐近线方程是
( )
的渐近线方程是
( )
(A)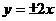 (B)
(B)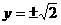 (C)
(C)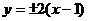 (D)
(D)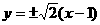
(3)设集合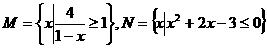 ,那么集合M与N之间的关系是
( )
,那么集合M与N之间的关系是
( )
(A)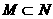 (B)M=N (C)
(B)M=N (C)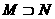 (D)
(D)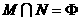
(4)4名男生2名女生站成一排,要求两名女生分别站在两端,则不同排法的种数为( )
(A)48 (B)96 (C)144 (D)288
(5)已知复数z=(t+i)2的辐角主值是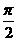 ,则实数t的值是
( )
,则实数t的值是
( )
(A)0 (B)-1 (C)1 (D)不能确定
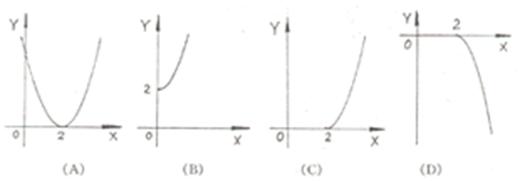
(6)函数f(x)=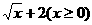 的反函数f-1(x)是图象是
( )
的反函数f-1(x)是图象是
( )
(7)理料做:在极坐标系中,点A在曲线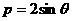 上,点B在曲线
上,点B在曲线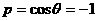 上,则
上,则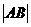 的最小值为
( )
的最小值为
( )
(A)0 (B)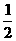 (C)
(C)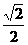 (D)1
(D)1
文科做:已知函数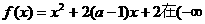 ,4]上是减函数,那么实数 a的取值范围是
( )
,4]上是减函数,那么实数 a的取值范围是
( )
(A)a≥–3 (B)a≤–3 (C)a≤5 (D)a≥3
(8)已知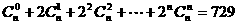 ,则
,则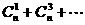 的值等于( )
的值等于( )
(A)64 (B)32 (C)63 (D)31
 (9)理科做:直线
(9)理科做:直线 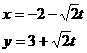 (t为参数)上到点A(-2,3)的距离等于
(t为参数)上到点A(-2,3)的距离等于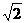 的一个点的坐标是
( )
的一个点的坐标是
( )
(A)(-2,3) (B)(-4,5)
(C)(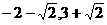 )
(D)(-3,4)
)
(D)(-3,4)
文科做:若k可以取任何实数,则方程x2+ky2=1所表示的曲线不可能是( )
(A)直线 (B)圆 (C)椭圆或双曲钱 (D)抛物线
(10)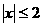 的必要但不充分条件是
( )
的必要但不充分条件是
( )
(A)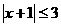 (B)
(B)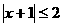 (C)
(C)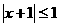 (D)
(D)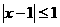
(11)已知集合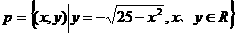 及
及
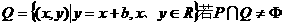 ,则实数b的取值范围是( )
,则实数b的取值范围是( )
(A)[–5,5] (B)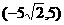 (C)
(C) (D)
(D)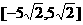
(12) a、b是异面直线,以下面四个命题:
①过a至少有一个平面平行于b ②过a至少有一个平面垂直于b
③至多有一条直线与a、b都垂直 ④至少有一个平面分别与a、b都平行
其中正确命题的个数是 ( )
(A)0 (B)1 (C)2 (D)3
(13)直线y=x cosα+1(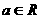 )的倾斜角的取值范围是
( )
)的倾斜角的取值范围是
( )
(A)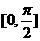 (B)[0,π]
(B)[0,π]
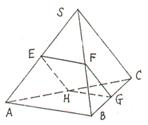 (C)
(C)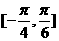 (D)
(D)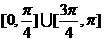
(14)三棱锥S-ABC,E、F、G、H分别是棱SA、SB、
BC、AC的中点,截面EFGH将三棱锥分割为两个几何
体:AB-EFGH、SC-EFGH,将其体积分别是V1、V2,
则V1∶V2的值是 ( )
(A)1∶2 (B)1∶3 (C)2∶3 (D)1∶1
高考命题注重考基础知识,考技能,反映基础知识的命题达百分之七十,但又要求有一定的难度,灵活度,综合度,这就要求复习不停留在知识的一般运用上,如函数是高考必考的内容,如2003年的高考中理解的第3、14、19,文科的第7、11、17题,理科的第6题实质也是二次函数的最值问题。这些题目体现由知识立意向能力立意转化,以知识为背景,突出能力的考查和思维的训练。要顺利解决这些问题,没有形成良好的函数,方程观点,是解决不了的。例如应用题的训练中,可以设计如图所示的思维线索
|
|

|
|

引导学生在面对新情景,新问题时,从有用信息提取入手,建立数学问题的模型,找出解决模型所需要的知识要求,方法。对得出的结果应检验。通过训练从而达到提高解决实际问题的能力。复习的最终目标毕竟要面向高考,通过复习使学生能够在心理、思维、体力等方面保持稳定、从容应对各种题目,最终取得优异成绩。
5、重视信息的反馈进行针对性讲评。
在高考复习阶段,学生要进行较多的练习与测验,我们不仅要精心设计安排学生训练,还要注意学生的反馈,在学生作业或考试后,做好五讲:即讲审题,讲思路,讲规律,讲延伸,讲答题技巧,此处以作业或考试,不要单给一个分数,因为分数只不过是学习成果的一种数量概括,它不能产生良好的反馈,最好提出指导性意见,让学生自己更正错误,也就是给学生“对未中之的,外射一箭”的机会。讲评要肯定成绩,指出问题,多鼓励、少指责,使学生重视自己的实际学习质量,激发他们改进愿望,促使他们产生新的学习动机,使自己的学习效果达到优化。
4、重视知识发展过程的复习。基础知识有其形成过程,相互间联系,切忌割裂,复习功夫要下在过程上,不应下在结果上。要结果不要过程是实用主义,这样知识无法转化能力。讲清过程能给予思想方法又能给予结果,学生对所掌握的知识就不容量忘记,即使忘记了,仍能自己推演出来,这就体现出知识变为能力。如数列的求和。应先讲清等差,特别是等比数列的前几项和公式的来源。从而引出求数列和的常用方法--错项相减法,倒序法。学生也能从体会公式的发明过程到记忆公式本身。
3、训练迁移。迁移力的高低反映创造力、灵活性的水平。对复杂的问题有人很快找到解题的路子,关键是找到联系,迁移的前提是找到联系,就是运用学过的规律知识,解决问题。如,2003年高考第16题考查正方体中一条对角线L与活动面MPN垂直的情况,若以推理方式处理,灵活性大,难度也大,若能迁移向量方法,则简洁易行。把近十多年使用迁移能力来解决的高考题,整理并形成系列发给学生进行练习,收效更好。
2、找出规律。目前我们还没有突出能力培养的教材,教材的这个缺陷迫使我们找出教材的规律,指导学生学会找规律。规律是客观存在的,是科学,要去找。例如三角函数这部分知识,学生都感觉到难,无从下手。我们应该引导学生从“角、名、形”三个字入手,角--已知的角与要求的角的和、差、倍、半的关系如何。名--化三角函数为同一名或尽量少的三角函数名。形--分式,多次幂,根式尽量化开。因此就把知识转化为能力,且知识本身的规律,能满足学生求知欲望,激发学生的稳定兴趣,能主动地投入这方面的研究,学生的能力又向更高层次发展。
高考改革已经由“知识立意”向“能力立意”转变,并将继续深入下去。在完成基础知识复习的前提下,学科能力的逐步培养和有针对性的训练是本阶段的首要任务,怎样把知识变成能力。
1、教学要形成观点。如数学有函数的观念,方程的观点等等,凡是变量之间的关系变化关系的问题,未知数求解,曲线的表示都可以用函数成方程的观点进行分析解决,形成观点的自觉性很重要,把观点交给学生,就能使学习自动控化。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com