
题目列表(包括答案和解析)
4.函数f(x)=ctgwx(w>0)图象的相邻两支截y=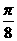 所得线段长为
所得线段长为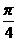 .则f(
.则f(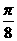 )的值是
)的值是
A.0
B.-1
C.1
D. 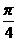
3.对于直线a、b和平面α、β,a∥b的一个充分条件是
A.a∥α,b∥α B.a∥α,b∥β,α∥β
C.a⊥α,b⊥β,α∥β D.α⊥β,a⊥α,b∥β
2.设α、β为钝角且sinα=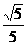 ,cosβ=-
,cosβ=-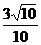 ,则α+β的值为
,则α+β的值为
A.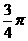 B.
B. 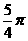 C.
C.
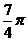 D.
D.
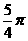 或
或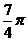
1.下面四个函数中,不存在反函数的函数的是
A.y=-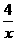 B.y=x4
C.y=3x
D.y=
B.y=x4
C.y=3x
D.y=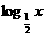
22.(本题满分14分)
已知PA⊥矩形ABCD所在平面,M、N分别是AB、PC中点.
(1)求证:MN⊥AB;
(2)设平面PDC和平面ABCD所成的二面角为锐角θ,问能否确定θ,使得直线MN为异面直线AB与PC的公垂线,若能,求出对应的θ值;若不能,说明理由.
21.(本题满分12分)
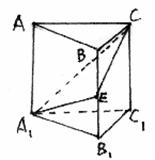
如图,在正三棱柱ABC-A1B1C1中,E∈BB1,截面A1EC⊥侧面AC1.
(1)求证:BE=EB1;
(2)若AA1=A1B1,求平面A1EC和平面A1B1C1所成二面角(锐角)的度数.
20.(本题满分12分)
已知直四棱柱ABCD-A1B1C1D1底面是矩形,又A1A=AB,E、F分别是BD1和AD中点.
(1)求异面直线CD1、EF所成的角;
(2)证明EF是异面直线AD和BD1的公垂线;
(3)若M为B1C1中点,求证:平面A1FCM⊥平面BCD1.
19.(本题满分12分)
已知正四棱柱ABCD-A1B1C1D1,底面边长为3,侧棱长为4,连CD1,作C1M⊥CD1,交DD1于M.
(1)求证:BD1⊥平面A1C1M;
(2)求二面角C1-A1M-D1的大小.
18.(本题满分12分)
已知三棱锥P-ABC的底面是边长为a的正三角形,PC⊥底面ABC,PC=a,O、E分别为棱AC、PA中点.
(1)求证:平面EBO⊥平面ABC;
(2)求点E到平面PBC的距离.
17.(本题满分12分)
长方体ABCD-A1B1C1D1中,M、N分别为棱AB和对角线A1C的中点.
(1)求证:MN⊥AB;
(2)若MN是异面直线AB、A1C的公垂线,求二面角A1-DC-A的度数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com