
题目列表(包括答案和解析)
7.下列各组命题中,命题M是命题N成立的充要条件的一组命题是
A.M:a>b;N:ac2>bc2
B.M:a>b,c>d;N:a-d>b-c
C.M:a>b>0,c>d>0;N:ac>bc
D.M:|a-b|=|a|+|b|;N:ab≤0
6.在①②③④中,能得出a与b一定共线的是
①a=1-2e,b=3e ②a=e1-e2,b=-e1+ e 2 ③a=2e1-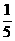 e2,b=e1-
e2,b=e1- e2
e2
④a=e1+ e 2,b=e1-e 2
A.①② B.②③ C.①③ D.①④
5.若不等式x2-2ax+a>0对x∈R恒成立,则关于t的不等式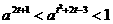 的解为
的解为
A.1<t<2 B.-2<t<1
C.-2<t<2 D.-3<t<2
4.已知|a|=8,|b|=15,|a+b|=17,则a与b的夹角θ为
A.0 B.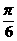 C.
C.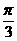 D.
D.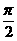
3.已知锐角三角形的三边分别为2、3、x,则x的取值范围是
A.1<x<5 B.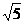 <x<
<x<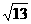
C.0<x<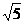 D.
D.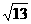 <x<5
<x<5
2.下列命题中,正确的是
A.若|a|=|b|,则a=b或a=-b
B.若a与b共线,则存在惟一实数λ,使a=λb
C.若a·b=0,则a=0或b=0
D.若|a-b|=|a|+|b|,则a与b共线
1.将函数y=cos2x的图象F按向量a=(-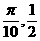 )平移到L,则L的函数解析式是
)平移到L,则L的函数解析式是
A.y=cos(2x+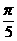 )+
)+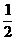 B.y=cos(2x-
B.y=cos(2x-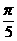 )+
)+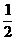
C.y=cos(2x+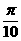 )+
)+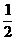 D.y=cos(2x-
D.y=cos(2x-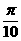 )+
)+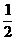
22.解:(1)函数f(x)在[-1,1]上是增函数.
证明:设任意x1,x2∈[-1,1],且x1<x2.
由于f(x)是定义在[-1,1]上的奇函数,
∴f(x2)-f(x1)=f(x2)+f(-x1). 2分
因为x1<x2,所以x2+(-x1)≠0,由已知有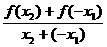 >0,
>0,
∵x2+(-x1)=x2-x1>0
∴f(x2)+f(-x1)>0,
即f(x2)>f(x1),
所以函数f(x)在[-1,1]上是增函数. 5分
(2)由不等式f(x+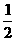 )<f(
)<f(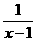 )得
)得
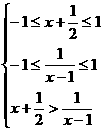 ,
,
解得-1<x<0,即为所求. 10分
(3)由以上知f(x)最大值为f(1)=1,所以要f(x)≤m2-2pm+1对所有x∈[-1,1],p∈ [-1,1](p是常数)恒成立,只需1≤m2-2pm+1恒成立,得实数m的取值范围为m≤0或m≥2p. 14分
21.解:(1)由已知得an+2-an+1=an+1-an(n∈N*),故{an}为首项14,公差为-12的等差数列,an=26-12n. 2分
(2)S1=14;S2=16;当n≥3时,Sn=a1+a2-(a3+a4+…+an)=16-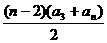 =6n2-20n+32 7分
=6n2-20n+32 7分
(3)因数列{bn}各项为正,所以Tn是递增的,要使得对任意n∈N*,均有Tn>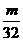 成立,只需T1>
成立,只需T1>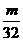 即可,由此得m<8.故存在最大整数m=7,使得任意n∈N*,均有Tn>
即可,由此得m<8.故存在最大整数m=7,使得任意n∈N*,均有Tn>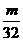 成立. 12分
成立. 12分
20.解:(1)若a<9,根据题中所给表得:
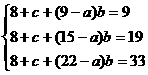 2分
2分
前两个式子相减得b= ,后两个式子相减得b=2,相互矛盾,故a<9不可能. 4分
,后两个式子相减得b=2,相互矛盾,故a<9不可能. 4分
若9≤a<15,根据题中所给表得:
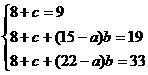 解得
解得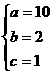 8分
8分
若15≤a<22,根据题中所给表得:
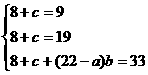 无解.
无解.
若a≥22,根据题中所给表得: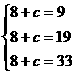 无解.
无解.
综合以上得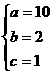 . 10分
. 10分
|
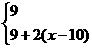 12分
12分湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com