
题目列表(包括答案和解析)
22.解:(1)不等式|x+3|>2|x|①的解集为A={x|-1<x<3,x∈R};不等式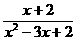 ≥1②的解集为B={x|0≤x<1或2<x≤4,x∈R}则A∩B={x|0≤x<1或2<x<3}. 4分
≥1②的解集为B={x|0≤x<1或2<x≤4,x∈R}则A∩B={x|0≤x<1或2<x<3}. 4分
设不等式③的解集为C,由题意知A∩B C
C
当m>0时,得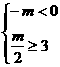 ,∴m≥6;
,∴m≥6;
当m=0时,C是空集,不合题意;
当m<0时,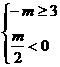 ,∴m≤-3.
,∴m≤-3.
由此得m≤-3或m≥6. 8分
(2)由(1)知A∪B={x|-1<x≤4};
由题意知C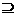 A∪B 10分
A∪B 10分
当m>0时,得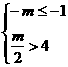 ,∴m>8;
,∴m>8;
当m=0时,C是空集,不合题意;
当m<0时,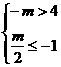 ,∴m<-4.
,∴m<-4.
由此得m<-4或m>8. 14分
21.解:当a+3<0即a<-3时,|3-a|>|a+3|,∴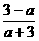 <-1, 3分
<-1, 3分
由此得不等式的解集为{x|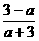 <x<-1,x∈R}; 5分
<x<-1,x∈R}; 5分
当a+3=0,即a=-3时,不等式解集为{x|x<-1,x∈R}; 7分
当a+3>0时,由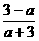 -(-1)=
-(-1)=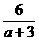 >0知
>0知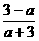 >-1, 10分
>-1, 10分
所以a>-3时原不等式解集为{x|x<-1或x>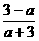 ,x∈R}. 12分
,x∈R}. 12分
20.解:(1)由题意知5×100+100n=50nx 3分
(2)设总损失费用为y元,则
y=125nx+100x+60(n+5)×100 7分
由(1)知n=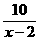 ,代入上式并整理得:
,代入上式并整理得:
y=31450+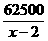 +100(x-2)≥31450+2
+100(x-2)≥31450+2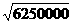 =36450(元) 10分
=36450(元) 10分
上式等号成立时,当且仅当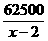 =100(x-2)时.
=100(x-2)时.
所以当x=27时,才能使总损失最小. 12分
19.解:(1)设a=n-1,b=n,c=n+1(n∈N*且n≥2) 2分
因C是钝角,
所以cosC=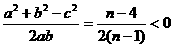 , 4分
, 4分
所以1<n<4,∴n=2或3
当n=2时,a=1,b=2,c=3,不能构成三角形;
当n=3时,a=2,b=3,c=4,cosC=-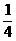 ,
,
∴C=π-arccos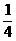 .即C=arccos(-
.即C=arccos(-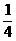 ). 8分
). 8分
(2)设夹角C的两边为x,y,则x+y=4
平行四边形的面积S=xysinC=x(4-x)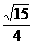 ,∴当x=2时,Smax=
,∴当x=2时,Smax= . 12分
. 12分
∴(ka-b)·(a-kb)=0. 2分
∴ka2-k2a·b-b·a+kb2=0.
∴9k-(k2+1)×3×2·cos120°+4k=0.
∴3k2+13k+3=0.
∴k=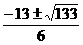 . 5分
. 5分
∴当k=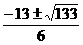 时,ka-b与a-kb垂直. 6分
时,ka-b与a-kb垂直. 6分
(2)∵|ka-2b|2=k2a2-4ka·b+4b2
=9k2-4k×3×2·cos120°+4×4
=9k2+12k+16=(3k+2)2+12. 10分
∴当k=-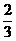 时,|ka-2b|取得最小值为2
时,|ka-2b|取得最小值为2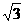 . 12分
. 12分
18.解:由余弦定理,得c2=a2+b2-2abcosC.
∵a2+b2=c2+ab,
∴ab-2abcosC=0.
∴cosC=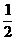 ,
,
∴C=60° 4分
∵sinAsinB=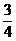 ,cos(A+B)=cos(180°-C)=cos120°=-
,cos(A+B)=cos(180°-C)=cos120°=-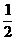 ,
,
cos(A+B)=cosAcosB-sinAsinB,
∴cosAcosB=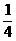 . 8分
. 8分
∴cos(A-B)=cosAcosB+sinAsinB=1.
∵-π<A-B<π,∴A-B=0.
∴A=B=60°.
∴△ABC是等边三角形. 12分
22.(本小题满分14分)
已知不等式|x+3|>2|x|①,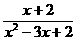 ≥1②,2x2+mx-m2<0③.
≥1②,2x2+mx-m2<0③.
(1)若同时满足不等式①、②的x值也满足不等式③,求m的取值范围;
(2)若满足不等式③的x值至少满足不等式①、②中的一个,求m的取值范围.
高三数学(文)全国统一标准测试(二)答案
21.(本小题满分12分)
a是任意的实数,解关于x的不等式(a+3)x2+2ax+a-3>0.
20.(本小题满分12分)
森林失火,火势以每分钟100 m2的速度迅速蔓延,消防队接到报警后立即派消防队员前去,在失火5分钟后赶到现场开始灭火.已知每位消防队员每分钟可灭火50 m2,所消耗的灭火材料等费用每人每分钟125元,另加每次灭火所消耗的车辆、器材和装备等费用平均每人100元,而每烧毁1 m2的森林直接损失费用为60 元,设消防队派x名消防队员前去救火,从到现场直至把火完全扑灭共用n分钟.
(1)写出x与n的关系式;
(2)问x为何值时,才能使总损失最小?
19.(本小题满分12分)
在△ABC中,三边a,b,c为连续正整数,最大角是钝角.
(1)求最大角;
(2)求以它的最大角为内角,夹此角的两边和为4的平行四边形的最大面积.
18.(本小题满分12分)
在△ABC中,a2+b2=c2+ab,且sinAsinB=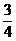 ,试判定△ABC的形状.
,试判定△ABC的形状.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com