
题目列表(包括答案和解析)
2.使集合M={x|ax2+2x+a=0,a∈R}中有且只有一个元素的所有a的值组成的集合N的子集个
数为 ( )
A.2 B.4 C.7 D.8
 3.已知函数f(x)=ax3+bx2+cx+d的图象如右图,则 ( )
3.已知函数f(x)=ax3+bx2+cx+d的图象如右图,则 ( )
A.b∈(-∞,0)
B.b∈(0,1)
C.b∈(1,2)
D.b∈(2,+∞)
项符合题目要求.)
1.已知x1是方程x+lgx=3的根,x2是方程x+10x=3的根,则x1+ x2等于 ( )
A.6 B.3 C.2 D.1
22.(本小题满分14分)
已知 ,
,
(1)设 的通项;
的通项;
(2)求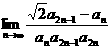 ;
;
(3)设 是否存在整数m,对一切n∈N*,都有
是否存在整数m,对一切n∈N*,都有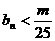 成立?若存在,求出m的最小值;若不存在,请说明理由.
成立?若存在,求出m的最小值;若不存在,请说明理由.
(3)两个公司在市场上相互竞争与联合垄断相比,哪一种情况对购买这种产品的消费者不利?请证明你的结论。
21.(本小题12分)
函数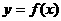 是偶函数,且是周期为2的周期函数,当x∈[2,3]时,
是偶函数,且是周期为2的周期函数,当x∈[2,3]时, ,在
,在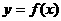 的图象上有两点A、B,它们的纵坐标相等,横坐标都在区间[1,3]上,定点C的坐标为(0,a)(其中a>2),求△ABC面积的最大值.
的图象上有两点A、B,它们的纵坐标相等,横坐标都在区间[1,3]上,定点C的坐标为(0,a)(其中a>2),求△ABC面积的最大值.
20.(本小题满分12分)
产品进入市场,满足的销售规律是价格越高,销售量越少。若某产品的价格为每吨p万元,销售量为q吨,则p与q满足关系 ,
,
(1)若该产品在某地市场被一个公司垄断,试说明该公司为获得最大收入,不会一味追求价格的提高,并求出收入最大时该产品的价格;
(2)若该产品由甲、乙两家公司销售,它们的销售量分别记作q甲、q乙,于是
19.(本小题12分)
数列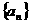 的通项公式
的通项公式
(1)求:f(1)、f(2)、f(3)、f(4)的值;
(2)由上述结果推测出计算f(n)的公式,并用数学归纳法加以证明.
18.(本小题12分)
一出租车司机从饭店到火车站途中有六个交通岗,假设他在各交通岗到红灯这一事件是
相互独立的,并且概率都是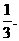
(1)求这位司机遇到红灯前,已经通过了两个交通岗的概率;
(2)求这位司机在途中遇到红灯数ξ的期望和方差。
17.(本小题12分)
求函数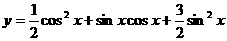 的最小正周期.
的最小正周期.
16.函数 在
在 上的最大值是
.
上的最大值是
.
15.已知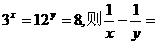 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com