
题目列表(包括答案和解析)
4.抛物线y2=4x的经过焦点的弦的中点轨迹方程是_________.
3.若实数x,y满足x2+y2-2x+4y=0,则x-2y的最大值为
A.5 B.10 C.9 D.5+2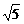
2.点P与两定点F1(-a,0)、F2(a,0)(a>0)的连线的斜率乘积为常数k,当点P的轨迹是离心率为2的双曲线时,k的值为
A.3 ? B.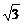 C.±
C.±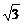 D.4
D.4
1.点P为双曲线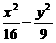 =1上异于顶点的任意一点,F1、F2是双曲线两焦点,则△PF1F2重心轨迹方程是
=1上异于顶点的任意一点,F1、F2是双曲线两焦点,则△PF1F2重心轨迹方程是
A.9x2-16y2=16(y≠0) B.9x2+16y2=16(y≠0)
C.9x2-16y2=1(y≠0) D.9x2+16y2=1(y≠0)
5.(满分20分)某城市准备举行书画展览,为了保证展品安全,展览的保卫部门准备安排保安员值班。情况如下:
①展览大厅是长方形,内设均匀颁的m×n个长方形展区,如图所示(下图是一个3×4个展区的示意图)。在展厅中,展览的书画被挂在每个展区的外墙上,参观者在通道上浏览书画。
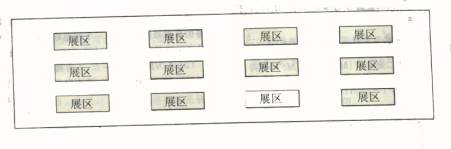
② 保安员站在固定的位置上,不允许转身,只能监视他的左右两侧和正前方,形如“T”形的区域。且一个保安员的正前方不安排其它保安员。
③ 不考虑保安员的轮岗、换班问题。
④ 展口的安全意味着每一个展区的四面外墙都在保安员的监视范围内。
问题:(1)对于如上图所示的展厅中,最少需要几个保安员能使展品安全?在图中标明保安员的位置(不要求证明)。
(2) 假如展要有n×m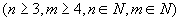 个展区,最少需要多少个保安员能使展品安全?请证明你的结论。
个展区,最少需要多少个保安员能使展品安全?请证明你的结论。
4.(满分20分)2000年末,某商家迎来店庆,为了吸引顾客,采取“满一百送二十,连环送”的酬宾方式,即顾客在店内花钱满100元(这100元可以是现金,也可是奖励券,或二者合计),就送20元奖励券;满200元,就送40元奖励券,满300元,就送60元奖励券;...。当日,花钱最多的一顾客用现金70000元,如果按照酬宾方式,他最多能得到多少优惠呢?相当于商家打了几折销售?
或演算步骤.
(17)(本小题满分10分)
已知复数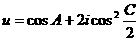 ,其中A、C为△ABC的内角,且三个内角
,其中A、C为△ABC的内角,且三个内角
满足2B=A﹢C.试求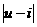 的取值范围.
的取值范围.
(18)(本小题满分12分)
已知曲线C上的任一点M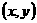 (其中
(其中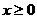 ),到点
),到点 的距离减去它到
的距离减去它到
y轴的距离的差是2,过点A的一条直线与曲线C交于P、Q两点,通过点P和坐标原点的直线交直线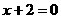 于N.
于N.
(I)求曲线C的方程;
(II)求证:NQ平行于x轴.
(19)(本小题满分12分)
是否存在一个等差数列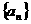 ,使对任意的自然数n,都有
,使对任意的自然数n,都有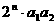 …
…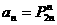 .
.
 (20)(本小题满分12分)
(20)(本小题满分12分)
如图,△ABC是一个遮阳棚,点A、B是地面上
南北方向的两定点,正西方向射出的太阳(用点
O表示)光线OCD与地面成锐角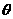 .
.
(I)遮阳棚与地面成多少度的二面角时,
才能使遮影△ABD面积最大?
(II)当AC=3,BC=4,AB=5,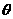 =30°时,试求出遮影△ABD的最
=30°时,试求出遮影△ABD的最
大面积.
 (21)(本小题满分14分)
(21)(本小题满分14分)
甲、乙、丙三种食物维生素A、B含量及成本如下表:
|
项 目 |
甲 |
乙 |
丙 |
|
维生素A(单位/千克) |
600 |
700 |
400 |
|
维生素B(单位/千克) |
800 |
400 |
500 |
|
成本(元/千克) |
11 |
9 |
4 |
某食物营养研究所想用x千克甲种食物、y千克乙种食物、z千克丙种食物
配成100千克混合物,并使混合物至少含有56000单位维生素A和63000
单位维生素B.试用x、y表示混合物的成本M(元);并确定x、y、z的值,
使成本最低.
(22)(本小题满分14分)
定义在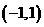 上的函数
上的函数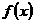 满足:①对任意
满足:①对任意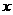 、
、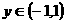 ,都有
,都有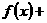
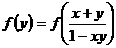 ;
;
②当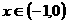 时,有
时,有 .
.
证明:(I)函数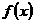 在
在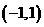 上的图象关于原点对称;
上的图象关于原点对称;
(II)函数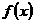 在
在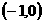 上是单调减函数;
上是单调减函数;
(III)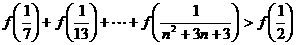 .
.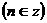
线上.
(13)函数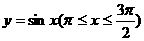 的反函数是
.
的反函数是
.
(14)已知抛物线的焦点坐标为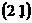 ,准线方程为
,准线方程为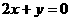 ,则其顶点坐标为
,则其顶点坐标为
 .
.
(15)如图,在棱长都相等的四面体A-BCD中,
E、F分别为棱AD、BC的中点,则直线
AF、CE所成角的余弦值为 .
(16)甲、乙、丙、丁、戊共5人参加某项技术比赛,决出了第1名到第5名
的名次. 甲、乙两名参赛者去询问成绩,回答者对甲说:“很遗憾,你
和乙都没拿冠军”,对乙说:“你当然不是最差的.”请从这个回答分析,
5人的名次排列共可能有 种不同情况(用数字作答).
(1)常数T满足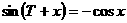 和
和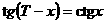 ,则T的一个值是( ).
,则T的一个值是( ).
(A)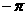 (B)
(B)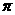 (C)
(C)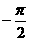 (D)
(D)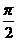
(2)在等差数列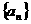 中,
中,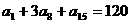 ,则
,则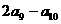 的值为( ).
的值为( ).
(A)24 (B)22 (C)20 (D)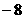
(3)设点P对应复数是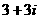 ,以原点为极点,实轴的正半轴为极轴,建立极坐
,以原点为极点,实轴的正半轴为极轴,建立极坐
标系,则点P的极坐标为( ).
(A) (B)
(B)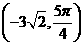 (C)
(C)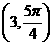 (D)
(D)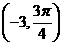
(4)设A、B是两个非空集合,若规定: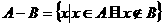 ,则
,则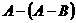
等于( ).
(A)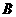 (B)
(B)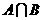 (C)
(C)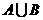 (D)
(D)
(5)函数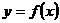 的图象与直线
的图象与直线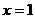 的交点个数为( ).
的交点个数为( ).
(A)0 (B)1 (C)2 (D)0或1
(6)设函数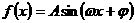 (其中
(其中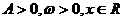 ),则
),则 是
是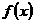 为
为
奇函数的( ).
(A)充分不必要条件 (B)必要不充分条件
(C)充要条件 (D)既不充分也不必要条件
 (7)如图,在斜三棱柱
(7)如图,在斜三棱柱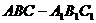 中,∠BAC=90°,
中,∠BAC=90°,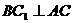 ,过
,过 作
作
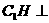 底面ABC,垂足为
底面ABC,垂足为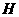 ,则( ).
,则( ).
(A)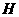 在直线AC上 (B)
在直线AC上 (B)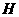 在直线AB上
在直线AB上
(C)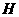 在直线BC上 (D)
在直线BC上 (D) 在△ABC内
在△ABC内
(8)电讯资费调整后,市话费标准为:通话时间不超过3分钟收费0.2元;超
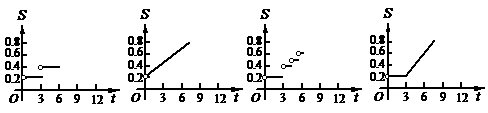 过3分钟,以后每增加1分钟收费0.1元,不足1分钟以1分钟收费.则通话收S(元)与通话时间t(分钟)的函数图象可表示为( ).
过3分钟,以后每增加1分钟收费0.1元,不足1分钟以1分钟收费.则通话收S(元)与通话时间t(分钟)的函数图象可表示为( ).
(A) (B) (C) (D)
(9)以椭圆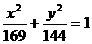 的右焦点为圆心,且与双曲线
的右焦点为圆心,且与双曲线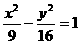 的渐近线相
的渐近线相
切的圆的方程为( ).
(A)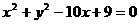 (B)
(B)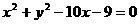
(C)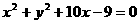 (D)
(D)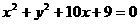
(10)已知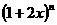 的展开式中所有项系数之和为729,则这个展开式中含
的展开式中所有项系数之和为729,则这个展开式中含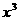 项
项
的系数是( ).
(A)56 (B)80 (C)160 (D)180
(11)AB是过圆锥曲线焦点F的弦,l是与点F对应的准线,则以弦AB为直
径的圆与直线l的位置关系( ).
(A)相切 (B)相交 (C)相离 (D)由离心率e决定
(12)定义在R上的函数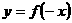 的反函数为
的反函数为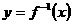 ,则
,则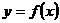 是( ).
是( ).
(A)奇函数 (B)偶函数
(C)非奇非偶函数 (D)满足题设的函数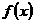 不存在
不存在
第II卷(非选择题共90分)
8. 设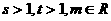 ,
,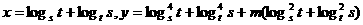 ,
,
(1)将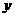 表示为
表示为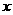 的函数
的函数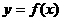 ,并求出
,并求出 的定义域;
的定义域;
(2)若关于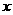 的方程
的方程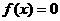 有且仅有一个实根,求
有且仅有一个实根,求 的取值范围.
的取值范围.
解:(1)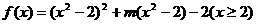
(2)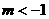
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com