
题目列表(包括答案和解析)
3.过抛物线的焦点F的直线与抛物线交于M、N两点,若M、N在抛物线的准线上的射影分别是M1、N1,则∠M1FN1等于
A.45° B.60° C.90° D.120°
2.过抛物线y2=4x的焦点作直线交抛物线于A(x1,y1)、B(x2,y2)两点,若x1+x2=6,那么|AB|等于
A.10 B.8 C.6 D.4
1.抛物线y=-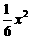 的准线方程为
的准线方程为
A.x=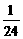 B.y=
B.y=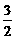
C.x=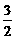 D.y=
D.y=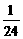
函数单调区间的合并主要依据是函数 在
在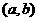 单调递增,在
单调递增,在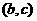 单调递增,又知函数在
单调递增,又知函数在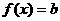 处连续,因此
处连续,因此 在
在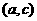 单调递增。同理减区间的合并也是如此,即相邻区间的单调性相同,且在公共点处函数连续,则二区间就可以合并为一个区间。
单调递增。同理减区间的合并也是如此,即相邻区间的单调性相同,且在公共点处函数连续,则二区间就可以合并为一个区间。
[例]用导数求函数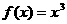 (
(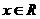 )的单调区间。
)的单调区间。
解:(用第一种关系及单调区间的合并)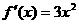 ,当
,当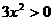 ,即
,即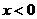 或
或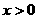 时,
时,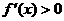 ∴
∴ 在
在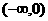 ,
,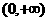 上为增函数,又∵
上为增函数,又∵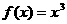 在
在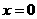 处连续,且相邻区间的单调性又相同,∴
处连续,且相邻区间的单调性又相同,∴ 在
在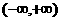 上为增函数。
上为增函数。
旧教材很少提到函数单调区间的合并,原因在于教师很难讲,学生很难把握,但是新教材引进函数的连续性和导数之后就很容易说明,也很容易理解了。
综之,用导数证明划分函数的单调性是导数最常用、也是最基本的应用,其它重要性如极值、最值等都必须用到单调性。它比用单调性的定义证明要简单许多,划分也容易理解得多。讨论可导函数得单调性可按如下步骤进行:
(1)
确定 的定义域;(2)求
的定义域;(2)求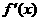 ,令
,令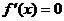 ,解方程求分界点;
,解方程求分界点;
(3)用分届点将定义域分成若干个开区间;
(4)判断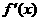 在每个开区间内的符号,即可确定
在每个开区间内的符号,即可确定 的单调性。
的单调性。
以下是前几年高考用导数证明、求单调性的题目,举例说明如下:
例1设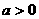 ,
,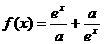 是
是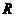 上的偶函数。
上的偶函数。
(I)求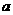 的值;(II)证明
的值;(II)证明 在
在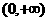 上是增函数。(2001年天津卷)
上是增函数。(2001年天津卷)
解:(I)依题意,对一切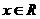 有
有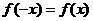 ,即
,即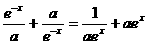 ,
,
∴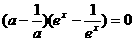 对一切
对一切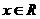 成立,由此得到
成立,由此得到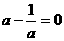 ,
,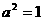 ,又∵
,又∵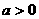 ,∴
,∴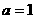 。
。
(II)证明:由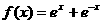 ,得
,得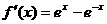
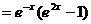 ,
,
当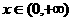 时,有
时,有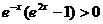 ,此时
,此时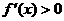 。∴
。∴ 在
在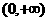 上是增函数。
上是增函数。
例2设函数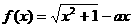 ,其中
,其中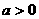 。(2000年全国、天津卷)
。(2000年全国、天津卷)
(I)解不等式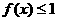 ;(II)证明:当
;(II)证明:当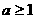 时,函数
时,函数 在区间
在区间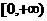 上是单调函数。
上是单调函数。
解1:(I)分类讨论解无理不等式(略)。 (II)作差比较(略)。
解2: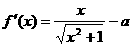 (i)当
(i)当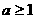 时,有
时,有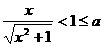 ,此时
,此时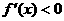 ,函数
,函数 在区间
在区间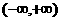 上是单调递减函数。但
上是单调递减函数。但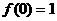 ,因此,当且仅当
,因此,当且仅当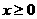 时,
时,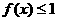 。
。
(ii)当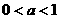 时,解不等式
时,解不等式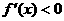 ,得
,得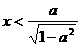 ,
, 在区间
在区间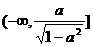 上是单调递减函数。解方程
上是单调递减函数。解方程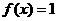 ,得
,得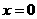 或
或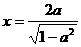 ,
,
∵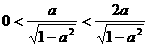 , ∴当且仅当
, ∴当且仅当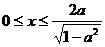 时,
时,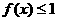 ,
,
综上,(I)当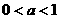 时,所给不等式的解集为:
时,所给不等式的解集为: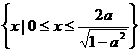 ;
;
当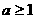 时,所给不等式的解集为:
时,所给不等式的解集为: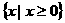 。
。
(II)当且仅当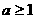 时,函数
时,函数 在区间
在区间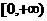 上时单调函数。
上时单调函数。
例3设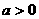 ,求函数
,求函数
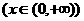 的单调区间。(2003年高考(理)19题)
的单调区间。(2003年高考(理)19题)
解: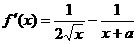 (
(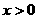 ) 当
) 当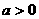 ,
,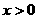 时,
时,
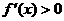

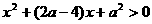 ,
,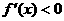

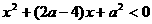 ,
,
(i)当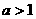 时,对所有
时,对所有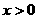 ,恒有
,恒有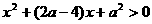 ,即
,即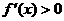 ,此时
,此时 在
在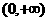 单调递增;
单调递增;
(ii)当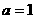 时,对
时,对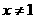 ,恒有
,恒有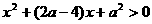 ,即
,即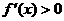 ,此时
,此时 在
在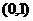 单调递增,在
单调递增,在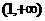 单调递增,
单调递增,
又知函数 在
在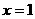 处连续,因此
处连续,因此 在
在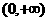 单调递增;
单调递增;
(iii)当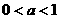 时,令
时,令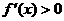 ,即
,即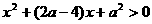 ,
,
解得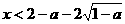 或
或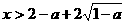 ,因此,函数
,因此,函数 在
在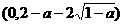 单调递增,在
单调递增,在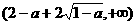 单调递增,令
单调递增,令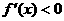 ,即
,即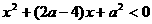 ,
,
解得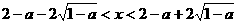 ,
,
因此,函数 在
在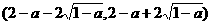 上单调递减。
上单调递减。
本题用传统作差比较法无法求函数的单调区间,只有用导数才行。
3.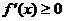 与
与 为增函数的关系。
为增函数的关系。
由前分析, 为增函数,一定可以推出
为增函数,一定可以推出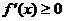 ,但反之不一定,因为
,但反之不一定,因为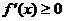 ,即为
,即为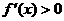 或
或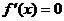 。当函数在某个区间内恒有
。当函数在某个区间内恒有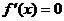 ,则
,则 为常数,函数不具有单调性。∴
为常数,函数不具有单调性。∴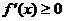 是
是 为增函数的必要不充分条件。
为增函数的必要不充分条件。
函数的单调性是函数一条重要性质,也是高中阶段研究的重点,我们一定要把握好以上三个关系,用导数判断好函数的单调性。因此新教材为解决单调区间的端点问题,都一律用开区间作为单调区间,避免讨论以上问题,也简化了问题。但在实际应用中还会遇到端点的讨论问题,特别是研究以下问题时。
2.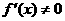 时,
时,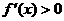 与
与 为增函数的关系。
为增函数的关系。
若将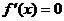 的根作为分界点,因为规定
的根作为分界点,因为规定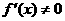 ,即抠去了分界点,此时
,即抠去了分界点,此时 为增函数,就一定有
为增函数,就一定有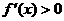 。∴当
。∴当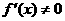 时,
时,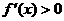 是
是 为增函数的充分必要条件。
为增函数的充分必要条件。
我们在应用导数判断函数的单调性时一定要搞清以下三个关系,才能准确无误地判断函数的单调性。以下以增函数为例作简单的分析,前提条件都是函数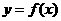 在某个区间内可导。
在某个区间内可导。
1.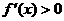 与
与 为增函数的关系。
为增函数的关系。
由前知,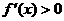 能推出
能推出 为增函数,但反之不一定。如函数
为增函数,但反之不一定。如函数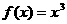 在
在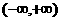 上单调递增,但
上单调递增,但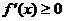 ,∴
,∴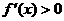 是
是 为增函数的充分不必要条件。
为增函数的充分不必要条件。
等积转化,亦称等积变换。通常是指用不同的方式求同一几何体的体积(或同一平面图形的面积)
例4. (’98全国高考)已知斜三棱柱,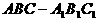 的侧面
的侧面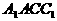 与底面垂直,
与底面垂直,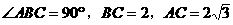 且
且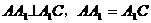 ,(如图7)
,(如图7)
(III)求C到侧面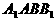 的距离。
的距离。
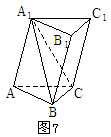
分析:连结A1B、A1C,过A1作AC的垂线A1D,D为垂足,由题意可知A1D⊥面ABC。根据定义,点C到面A1AAB1的距离,即为三棱锥C-A1AB的高h。
由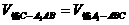 得:
得:
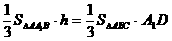
即: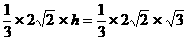
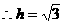 为所求
为所求
例5. (’92全国高考)如图8,已知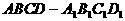 是棱长为a的正方体,E、F分别为棱
是棱长为a的正方体,E、F分别为棱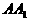 与
与 的中点,求四棱锥
的中点,求四棱锥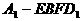 的体积。
的体积。
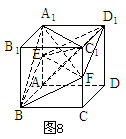
分析:
易证四边形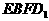 为菱形,连结
为菱形,连结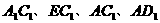 ,则
,则

说明:利用等积变换既可求得有关几何体的体积,又可避开作出点到平面的距离而直接求出。
总之,立体几何问题联系多多,变化多多,但只要能对其进行合理而有效的转化,便可使问题浮出水面,看得见,摸得着。
由三维空间向二维空间转化,是研究立体几何问题最重要的数学方法之一。在解决实际问题中,往往通过一定手段,将空间问题转化成平面问题,得以解决。
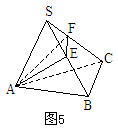
例3. 如图5,设正三棱锥S-ABC的底面边长为a,侧棱长为2a,过A作与侧棱SB、SC都相交的截面AEF,求这个截面周长的最小值。
分析:沿侧棱SA将三棱锥的侧面展开如图6,求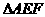 周长最小值问题就转化成了求A、A'两点间的最短距离。
周长最小值问题就转化成了求A、A'两点间的最短距离。
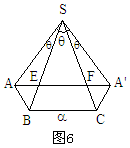
设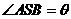 ,则由余弦定理得
,则由余弦定理得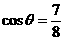
所以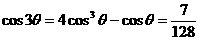
可求得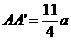
即所求截面周长的最小值为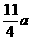
说明:这类问题通常都是将几何体的侧面展开,空间问题转化成平面问题来解决。
割·补转化是通过割与补,来改变几何体的状态,由复杂几何体变为简单几何体的数学方法。
例2. (’87全国高考)如图2,三棱锥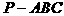 中,已知
中,已知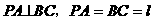 ,PA、BC的公垂线段
,PA、BC的公垂线段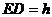 ,求证三棱锥
,求证三棱锥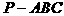 的体积
的体积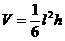 。
。
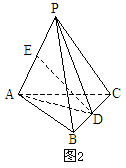
分析一:
如图2,连结AD、PD,
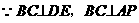
 平面APD,又
平面APD,又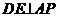 ,
,
∴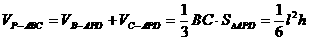
分析二:
如图3,以三棱锥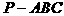 的底面为底面,侧棱PA为侧棱,补成三棱柱
的底面为底面,侧棱PA为侧棱,补成三棱柱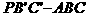 ,连结EC、EB,则易证AP⊥平面EBC,
,连结EC、EB,则易证AP⊥平面EBC,
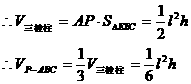
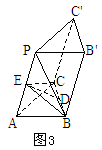
分析三:
如图4,将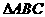 补成平行四边形ABCF,可利用
补成平行四边形ABCF,可利用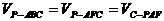
易得:
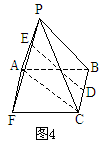
说明:割·补转化是解决立体几何问题常用的方法之一,对同一几何体既可进行合理分割,又可实施有效的添补。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com