
题目列表(包括答案和解析)
2.已知非空集合A={x|2a+1≤x≤3a-5},B ={x|3≤x≤22},则能使AÍA∩B成立的a的取值范围是 ( )
A.{a|1≤a≤9} B.{a|6≤a≤9} C.{a|a≤9} D.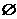
1.若以集合S={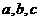 }中的三个不同元素为边长可构成一个三角形,那么这个三角形一定不可能是
( )
}中的三个不同元素为边长可构成一个三角形,那么这个三角形一定不可能是
( )
A.锐角三角形 B.直角三角形
C.钝角三角形 D.等腰三角形
5.用集合思想解题
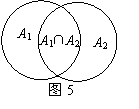 [例11]一次大型会议有2002位代表参加,每位代表至少有1335位合作者.试问这些代表中是否总可以找到四位代表,他们中的每两位都合作过?请证明你的结论.
[例11]一次大型会议有2002位代表参加,每位代表至少有1335位合作者.试问这些代表中是否总可以找到四位代表,他们中的每两位都合作过?请证明你的结论.
[分析]以合作的人数最少(2人)的情况为基础,构造集合,利用集合元素的个数的计数原理,使合作的人数增多.
[解]记各代表为ai(i=1,2,3,…,2002),与ai合作过的代表组成的集合记为Ai,任取合作过的两位代表为a1,a2,于是
card(A1)≥1335,card(A2)≥1335,
card(A1∪A2)≤2002,card (A1∪A2∪A3)≤2002.
画出韦恩图(如图5),得
card(A1∩A2)= card(A1)+ card(A2)- card(A1∪A2)
≥1335+1335-2002=668>0,
从而,存在代表a3Î A1∩A2,且a3Ï{ a1,a2}.
又card(A1∩A2∩A3)= card[(A1∩A2)∩A3]
= card(A1∩A2)+ card(A2)- card[(A1∩A2)∪A3]
≥668+1335- card[(A1∪A2)∪A3] ≥2003-2002=1.
于是,存在代表a4Î A1∩A2∩A3,且a4Ï{ a1,a2,a3},即存在代表a1,a2, a3, a4,两两合作过.
[点悟]①解题关键点是构造集合,利用集合思想进行解题.
②解题规律是画韦恩图,得到关于集合的元素个数的计数原理:card(A∩B)= card(A)+ card(B)- card(A∪B).
利用集合思想解题,使问题变得简洁,思路显得清晰.
③解题易错点容易误认为:card(A∪B)= card(A)+ card(B).
4.分类讨论法
[例8]已知三个集合A={x∣x2-3x+2=0},B={x∣x2-ax+a=1},C={x∣x2-bx+2=0}.试问同时满足B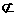 A且C?A的实数a和b是否存在?若存在,求出a,b的所有值;若不存在,请说明理由.
A且C?A的实数a和b是否存在?若存在,求出a,b的所有值;若不存在,请说明理由.
[分析]先化简集合A、B及C,然后运用条件B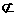 A且C?A探求a与b的值或说明其不存在.
A且C?A探求a与b的值或说明其不存在.
[解]由 x2-3x+2=0,解得 x=1或x=2,于是A={1,2}.
由x2-ax+a=1,解得 x=1或x=a -1.于是,
当a=2时,B={1};当a≠2时,B={1,a-1}.
先求实数a的可能取值:
当a=2,即B={1}时,不满足B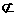 A,故a≠2;
A,故a≠2;
当B={1,a-1},即a≠2时,由B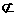 A,得a-1≠2,于是a≠3.
A,得a-1≠2,于是a≠3.
其次求实数b的可能取值:
对于方程x2-bx+2=0,其判别式 ⊿=b2-8.
当⊿<0,即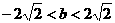 时,方程x2-bx+2=0无解,C=
时,方程x2-bx+2=0无解,C=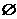 ,显然满足题设;
,显然满足题设;
当⊿=0,即b= 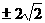 时,方程x2-bx+2=0的解为x=
时,方程x2-bx+2=0的解为x=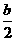 ,C={
,C={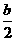 },即C={
},即C={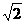 }(当b=
}(当b=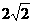 )或C={
)或C={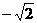 }(当b=
}(当b=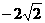 ),此时,不能满足C?A,故b≠
),此时,不能满足C?A,故b≠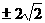 ;
;
当⊿>0,即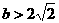 或
或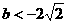 时,方程x2-bx+2=0有两个不等实数根
时,方程x2-bx+2=0有两个不等实数根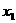 、
、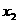 ,于是C={
,于是C={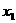 ,
,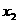 }.若C?A,则必有1∈C或2∈C.但
}.若C?A,则必有1∈C或2∈C.但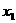 ·
·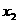 =2,故
=2,故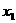 、
、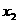 均不能为1或2,从而此种情形下无解.
均不能为1或2,从而此种情形下无解.
故满足条件的实数a与b均存在,且a∈R,a≠2、3,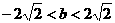 .
.
[点悟]①解题关键点是弄清每一个集合中的元素,理清集合间的关系,正确合理使用题中所给信息,对问题所及方面进行正确的分类.
②解题技巧是对集合A、B与C的化简及对集合A与B的分别求解.
③解题易错点是忽视对集合元素的互异性的检验,遗漏空集是任何非空集合的真子集的情形,忽视对集合B的元素个数是一个还是两个的讨论.
[例9]设集合A={x∣x2+px+1=0},B={ x∣x >0},当A∩B=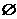 ,求实数p的取值范围.
,求实数p的取值范围.
[分析]利用根的判别式与0的大小关系分A为空集和非空集的情况讨论求解.
[解]因 A∩B=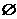 ,故 A=
,故 A=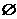 或A中的元素只有非正数.
或A中的元素只有非正数.
若A=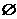 ,则⊿=p2-4<0,解得 -2< p<2;
,则⊿=p2-4<0,解得 -2< p<2;
若A中的元素只有非正数,则 ⊿≥0且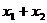 = -p≤0,
= -p≤0,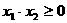 ,解得 p≥2.
,解得 p≥2.
于是实数p的取值范围为p>-2.
[点悟]①解题关键点是将集合语言准确地翻译成文字语言,即转换成一种更为直观浅显的条件.
②解题规律是对于含有参数的一元二次方程根的情况可使用判别式法进行讨论求之.
③解题易错点是忽视A=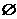 的情况,引起失解,缩小p的取值范围.
的情况,引起失解,缩小p的取值范围.
[例10]已知集合P= .
.
(1)若P中只有一个元素,试求a的值,并把这个元素写出来;
(2)若P中至多只有一个元素,试求a的取值范围.
[分析]x2前的系数为a,它在变化,故须对a进行讨论:它可能是一元一次方程,也可能是一元二次方程;它可能有实数根,也可能无实数根.
[解]集合P表示方程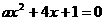 在实数范围内的解的集合.
在实数范围内的解的集合.
(1)当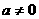 时,⊿=
时,⊿=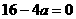 ,a =4,方程有两个相等的实数根
,a =4,方程有两个相等的实数根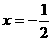 ,P中只有一个元素;当a=0时,方程为一元一次方程,方程只有唯一解
,P中只有一个元素;当a=0时,方程为一元一次方程,方程只有唯一解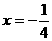 .故当P中只有一个元素时,a=4或0.当a=4时,元素为
.故当P中只有一个元素时,a=4或0.当a=4时,元素为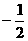 ;当a=0时,元素为
;当a=0时,元素为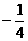 .
.
(2)P中至多只有一个元素,包含P为空集和P中只有一个元素两种情形.当P为空集时,由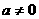 及⊿=
及⊿= 解得a>4,从而a的取值范围为
解得a>4,从而a的取值范围为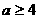 或a=0.
或a=0.
[点悟]①解题关键点是正确审题,搞清“只有一个”与“至多只有一个”的真正含义并注意它们的区别,注意参数a所在的位置(这里的a在二次项系数前,因而方程未必为二次的)对解题的影响.
②解题规律是根的判别式⊿只适用于实系数一元二次方程根的讨论.
③解题易错点是混淆“空集是不含任何元素的集合”的概念,从而遗漏对空集情况的检验讨论;另一方面容易忽视对方程次数即a=0的情况的讨论.
3.数形结合法
[例6](1)已知U为全集,集合M、N?U,若M∩N=N,则 ( )
A.?UM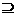 ?UN B.M
?UN B.M ?UN
?UN
C.?UM ?UN
D.M
?UN
D.M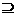 ?UN
?UN
(2)设U是全集,集合P、Q满足P?Q,则下面的结论中错误的是 ( )
A.P∪Q=Q B.(?U P)∪Q=U
C.P∩(?U Q)=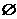 D.(?U P)∩(?U Q)=?U P
D.(?U P)∩(?U Q)=?U P
[分析]本题中两小题是一对姊妹题,一对高考题,第(1)小题为1995年全国高考题,检测根据集合的交并关系判断集合间
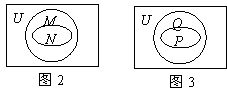 的包含及包含于关系;第(2)小题为1994年上海市高考题,检测由集合的包含关系判断集合的交并关系.两小题均涉及全集、补集、子集及真子集、集合的交并补运算,题中均未给出具体的集合,因而它们不仅全面检测了考生对集合概念理解和掌握程度,也检测了考生的抽象能力,是两道“题小功能大”的好题.对于第(1)小题,作出韦恩图如图2,由图易知?UM
的包含及包含于关系;第(2)小题为1994年上海市高考题,检测由集合的包含关系判断集合的交并关系.两小题均涉及全集、补集、子集及真子集、集合的交并补运算,题中均未给出具体的集合,因而它们不仅全面检测了考生对集合概念理解和掌握程度,也检测了考生的抽象能力,是两道“题小功能大”的好题.对于第(1)小题,作出韦恩图如图2,由图易知?UM ?UN正确,从而答案选C;对于第(2)小题,作出韦恩图如图3,由图可知,仅D选项的内容错误,从而答案选D.
?UN正确,从而答案选C;对于第(2)小题,作出韦恩图如图3,由图可知,仅D选项的内容错误,从而答案选D.
[点悟]①解题关键点是借助韦恩图法,直接观察得到结论.
②解题规律是当问题比较抽象时,可以将问题特殊化、具体化,不妨取些特例,即用选择题的特例排除法来迅速得到答案.如对于第(1)小题,可令U={1,2,3,4},M={1,2,3},N={1,2},则?UM={4},?UN={3,4},显然只有?UM ?UN成立,故答案非C莫属;对于第(2)小题,亦可令U={1,2,3,4},Q={1,2,3},P={1,2},则错误结论D跃然纸上.
?UN成立,故答案非C莫属;对于第(2)小题,亦可令U={1,2,3,4},Q={1,2,3},P={1,2},则错误结论D跃然纸上.
③解题易错点是读审题不认真仔细,不能注意提示用语,如第(1)小题选的是正确项,而第(2)小题选的则是错误项;另外不能正确理解集合语言及符号,搞错概念的内涵与外延.
[例7]已知集合A=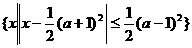 ,B=
,B=
{ x︱3a+1≤x≤2},试问是否存在实数a使得A Ì B成立?若存在,试求出a的值;若不存在,请说明理由.
[分析]本题检测解绝对值不等式的能力,对集合间的包含关系的理解和转化能力,以及对字母的分类讨论能力,是一道小型综合题.解题时,可先对集合A进行化简,然后根据集合间的关系利用数形结合的办法,画出数轴,求出适合题意的a的值,或说明其值不存在.
[解]根据︱x︱≤a(a>0)的解集可将A中的元素化为
 .
.
解得 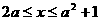 .
.
故
A={ x︱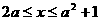 }.
}.
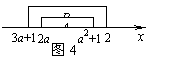 因A Ì B,画出如图4的示意图,由此得
因A Ì B,画出如图4的示意图,由此得
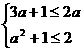
解得 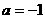 .
.
于是符合条件的实数a存在,且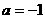 .
.
[点悟]①解题关键点是正确理解条件“A Ì B”,画出数轴,以形助数,从而顺利破解问题.
②解题规律是一般为先假设问题是存在的,然后通过计算、证明、推理等手段,能求出解的可下结论是存在的,不能求出其解的可下结论是不存在的.其解题过程和一般非开放型问题的求解相类似.
③解题易错点是认为有参数的问题,都需要讨论,而这里并非如此.
2.定义法
[例3]设集合M={直线},P={圆},则集合M∩P中的元素个数为 ( )
A.0 B.1 C.2 D.0或1或2
[分析]本题考查集合的交集与并集的运算,是一道概念性极强的试题,可使用定义法求解.
[解]因集合M={直线},P={圆},集合M∩P中的元素既是直线且又是圆,显然这样的元素不存在,从而M∩P=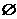 ,答案选A.
,答案选A.
[点悟]①解题关键点是正确理解集合的交集与并集的运算及M∩P的意义.集合的交集是由既属于集合A且又属于集合B的公共元素组成的集合,它强调的是“且”的关系;并集是由属于A或属于集合B之一的元素组成的集合,它强调的是“或”的关系.
②解题规律:定义法解题的一般步骤为:(ⅰ)分析和研究所给问题中已知的条件和待求的解题目标;(ⅱ)回忆有关概念的内涵和要点;(ⅲ)用定义去指导解题活动.
③解题易错点是将M∩P误认为是直线与圆的交点个数问题,从而误选D.本题若改为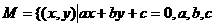 为常数,且a,b不同时为零},
为常数,且a,b不同时为零},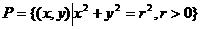 ,则M∩P中的元素个数应为0或1或2.
,则M∩P中的元素个数应为0或1或2.
[例4]已知集合A={a,b,c,d},B={a2,b2,c2,d2},其中A?N*,B?N*,a<b<c<d,且A∩B={a,d},a+d=10.
(1)求a、d;
(2)若A∪B中所有元素的和为124,你能确定集合A、B中的所有元素吗?
[分析](1)根据交集的意义及其题设,求解出a,d.
(2)由A∩B中的元素个数为2,而A与B的元素个数均为4个可知:A∪B中共有6个元素,且其中有四个元素分别为1,3,9,81,而另两个元素分别为x与x2.一个未知数,还有一个和的条件,可以求解x,进而可求得集合A与B.
[解](1)因A∩B={a,d},且a<b<c<d,于是 a= a2,解得 a=1(a=0,不合,舍去),从而 d=9.
(2)A={1,b,c,9},B={1,b2,c2,81}.
因 A∩B={1,9},故 3∈A,9∈B.
于是可设A={1,3,9,x},B={1,9,81,x2},其中x<9.
依题设有 1+3+9+x+81+ x2=124, 解得 x=5(x= -6,不合,舍去).
故 A={1,3,5,9},B={1,9,25,81}.
[点悟]①解题关键点是熟练掌握利用集合元素的三大特性(即集合元素的互异性、无序性、确定性)进行解题.
②解题规律:对于递进型的综合问题,应采取各个“击破”,“分而治之”,直至“歼灭”的办法.
③解题易错点求集合的并运算,不是两个集合所有元素的简单迭加;另外容易忽视集合元素的互异性,即相同的元素在一个集合中只算一个元素.
[例5]在下列电路图中,闭合开关A是灯泡B亮的什么条件:
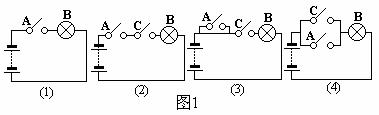 图1 (1)中,开关A闭合是灯泡B亮的 条件;
图1 (1)中,开关A闭合是灯泡B亮的 条件;
图1 (2)中,开关A闭合是灯泡B亮的 条件;
图1 (3)中,开关A闭合是灯泡B亮的 条件;
图1 (4)中,开关A闭合是灯泡B亮的 条件.
[分析]首先根据电路的串并联知识,分析开关A闭合是否有灯泡B亮,然后根据充分而不必要条件、必要而不充分条件、充要条件的含义作答.
[解](1)开关A闭合,灯泡B亮;反之,灯泡B亮,开关A闭合,于是开关A闭合是灯泡B亮的充要条件.
(2)仅当开关A、C都闭合时,灯泡B才亮;反之,灯泡B亮,开关A必须闭合,故开关A闭合是灯泡B亮的必要而不充分条件.
(3)开关A不起任何作用,故开关A闭合是灯泡B亮的既不充分又不必要条件.
(4)开关A闭合,灯泡B亮;但灯泡B亮,只须开关A或B闭合,故开关A闭合是灯泡B亮的充分而不必要条件.
[点悟]①解题关键点是正确理解充分与必要条件的含义,读懂图形语言,并掌握一些物理学知识特别是简单的电学知识,进行电路图的正确分析.
②“学以致用”已不是什么口号.重视知识的综合,体现时代的特点,渗透素质教育的内含,是一种大势所趋.
③解题易错点是对条件的充分与必要性区分不清,不能正确地读懂电路图.
1.化归与转化
[例1]已知集合A={2,3,5,6,8},B={1,3,5,7,10}.集合C满足:①若将C中的各元素均减2,则新集合C1就变为A的一个子集;②若将C中的各元素均加3,则新集合C2就变为B的一个子集;③C中的元素可以是一个一元二次方程的不等实数根.试根据以上条件,用列举法表示集合C.
[分析]本小题重点检测文字语言向符号语言转换的能力.条件③即就是集合C中的元素个数为2.从子集的定义出发,并将条件①、②分别转换成另一种表述方式,可使问题顺利求解.
[解]将①换一种说法,即若将A中的各个元素均加2,得新集合A1,则C A1,即C
A1,即C {4,5,7,8,10};将②换一种说法,即若将B中的各个元素均减3,得新集合B1,则C
{4,5,7,8,10};将②换一种说法,即若将B中的各个元素均减3,得新集合B1,则C B2,即C
B2,即C {-2,0,2,4,7}.于是C
{-2,0,2,4,7}.于是C ({4,5,7,8,10}∩{-2,0,2,4,7})={4,7}.又由条件③知,集合C中的元素恰有两个,于是C={4,7}.
({4,5,7,8,10}∩{-2,0,2,4,7})={4,7}.又由条件③知,集合C中的元素恰有两个,于是C={4,7}.
[点悟]①解题关键点是正确地将文字语言翻译成集合语言(或符号语言).
②解题规律是当直接求解不易时,可考虑问题的反面或换一种表述方式,如本题中将“C1为A的子集”换为“C1 A”,再换为“C
A”,再换为“C A1”;将“C2为B的子集”换为“C2
A1”;将“C2为B的子集”换为“C2 B”,再换为“C
B”,再换为“C B2”,这样迅速地破解了问题.
B2”,这样迅速地破解了问题.
③本题的一个拓广是:将条件③去掉,则问题便是求集合{4,7}的非空子集(想一想:为什么集合C不能为空集),答案为{4},或{7}或{4,7}.
[例2]设A=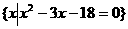 ,B=
,B= .
.
(1)若A∩B=B,试求实数a,b所满足的条件;
(2)若A∪B=B,试求实数a,b所满足的条件.
[分析]利用A∩B=B与B A的等价性及A∪B=B与A
A的等价性及A∪B=B与A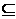 B的等价性将问题进行转化,注意分类讨论思想的运用.
B的等价性将问题进行转化,注意分类讨论思想的运用.
[解]解方程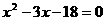 ,得 x= -3或x=6,于是A={-3,6}.
,得 x= -3或x=6,于是A={-3,6}.
(1)因A∩B=B,故B A,即B
A,即B {-3,6},从而B=
{-3,6},从而B=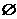 ,或B={-3},或B={6},或B={-3,6}.
,或B={-3},或B={6},或B={-3,6}.
若B=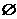 ,则方程
,则方程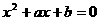 无实数解,于是⊿=
无实数解,于是⊿=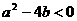 ;
;
若B={-3},即方程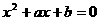 有相等的实数根且该根为x= -3.从而由韦达定理可得a= 6,b=9;
有相等的实数根且该根为x= -3.从而由韦达定理可得a= 6,b=9;
若B={6},即方程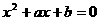 有相等的实数根且该根为x= 6.从而由韦达定理可得a=
-12,b=36;
有相等的实数根且该根为x= 6.从而由韦达定理可得a=
-12,b=36;
若B={-3,6},即方程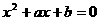 的两根为x= -3和 x=6.从而由韦达定理可得a= -3,b=
-18.
的两根为x= -3和 x=6.从而由韦达定理可得a= -3,b=
-18.
综合上面的讨论可知,当A∩B=B时,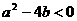 或a= 6,b=9或a=
-12,b=36或a= -3,b= -18.
或a= 6,b=9或a=
-12,b=36或a= -3,b= -18.
(2)因A∪B=B,故A B,即{-3,6}
B,即{-3,6} B.又B为一元二次方程的解集,故B中的元素最多只有两个,从而A=B,于是a= -3,b= -18.
B.又B为一元二次方程的解集,故B中的元素最多只有两个,从而A=B,于是a= -3,b= -18.
[点悟]①解题关键点是善于将A∪B=B等价转化为A B,将A∩B=B等价转化为B
B,将A∩B=B等价转化为B A .
A .
②解题规律是当已知方程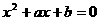 的两不等实数根时,除可使用韦达定理求解a、b外,还可直接将两根均代入方程得到关于a、b的二元方程组,然后求解方程组得出a、b的值;如方程
的两不等实数根时,除可使用韦达定理求解a、b外,还可直接将两根均代入方程得到关于a、b的二元方程组,然后求解方程组得出a、b的值;如方程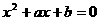 只有唯一的一个实数根m,则:实数根m满足方程且根的判别式为0.另外第(1)小题中的B={-3,6}的情形,也可这样求解:因B=A,故方程x2-3x-18=0与方程
只有唯一的一个实数根m,则:实数根m满足方程且根的判别式为0.另外第(1)小题中的B={-3,6}的情形,也可这样求解:因B=A,故方程x2-3x-18=0与方程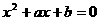 等价,利用对应项系数成比例即得a= -3,b=
-18.
等价,利用对应项系数成比例即得a= -3,b=
-18.
③解题易错点是遗漏空集亦满足性质:A∩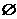 =
=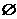 ;另外结论的表示混乱,如将第(1)小题的结论表示成a=6或a= -12或a=
-3,b=9或b=36或b= -18,及
;另外结论的表示混乱,如将第(1)小题的结论表示成a=6或a= -12或a=
-3,b=9或b=36或b= -18,及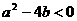 .
.
|
主干知识点 |
知能转化点 |
|
(1)集合、子集、全集、补集的概念 (2)空集和全集的意义 (3)元素与集合的关系;集合与集合的关系 (4)集合的表示法 (5)交集与并集的性质和运算 (6)逻辑联结词“或”、“且”、“否”的含义 (7)四种命题及相互关系 (8)充要条件 |
(1) 集合中的元素的三个特性,是判断一组对象能否组成一个集合的依据 (2)区分有关术语和符号,用符号语言正确表示有关的集合 (3)利用数形结合(包括韦恩图及数轴等)的思想方法,图示各集合间的关系并进行有关集合间的运算 (4)充要条件的判断及用反证法证题 |
|
解题关键点 |
常见障碍点 |
|
(1)理解集合概念,弄清元素与集合、集合与集合的关系 (2)弄清交、并集的区别与联系 (3)“AÍB”Û “A∩B=A”Û“A∪B=B”Û“AÍ A∩B” (4)结合转化思想、数形结合思想等用集合观点来解决“简易逻辑”中的问题 (5)“pÞq”Û{x|p}Í{x|q}”Û“{x|q}Ê{x|p}”Û“p是q的充分条件”Û“q是p的必要条件” |
(1)容易混淆∈与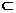 的区别 的区别(2)容易混淆a与{a}的区别 (3)容易混淆空集 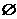 与集合{0}的区别 与集合{0}的区别(4)容易忽视空集为任何集合的子集、非空集合的真子集这一特例 (5)容易遗漏0为自然数的特例 (6)容易混淆充分条件与必要条件的区别 (7)容易混淆命题的否命题与命题的否定的区别 |
25.设a>0,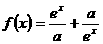 是R上的偶函数。
是R上的偶函数。
(1)求a的值;
(2)证明:f(x)在(0,+∞)上是增函数。
(2001天津理(19))
24.对于函数f(x),若存在x0∈R,使f(x0)=x0成立,则称x0为f(x)的不动点。已知函数f(x)=ax2+(b+1)x+(b-1) (a≠0)。
(1)当a=1,b=-2时,求函数f(x)的不动点;
(2)若对任意实数b,函数f(x)恒有两个相异的不动点,求a的取值范围;
(3)在(2)的条件下,若y=f(x)图象上A、B两点的横坐标是函数f(x)的不动点,且A、B两点关于直线y=kx+1/(2a2+1)对称,求b的最小值。
(2002上海春招(22))
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com