
题目列表(包括答案和解析)
21.当c∈(0, 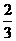 ]时, n=1; 当c∈(
]时, n=1; 当c∈(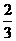 , 1)时, n=
, 1)时, n=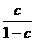 的整数部分或当
的整数部分或当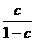 为整数时
为整数时
n=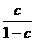 -1=
-1=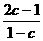 . 22.(1) an=n2-n+1; (2) Sn=n3; (3) (4) 用放缩法证明略
. 22.(1) an=n2-n+1; (2) Sn=n3; (3) (4) 用放缩法证明略
20.(1) f
-1(x)=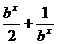 , 0<b<1时,定义域为(-∞, logb
, 0<b<1时,定义域为(-∞, logb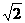 ],
],
b>1时,定义域为[logb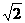 . +∞); (2) 1<b<3.
. +∞); (2) 1<b<3.
19.n≥2时,1+x+x2+……+xn<n+xn+1. 用数学归纳法证明
17.k≥2时, 解集为(-1, 1);0<k<2时, 解集为(1-k, 1). 18.证明略
13.[-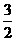 ,
, 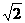 ) 14.(1,
) 14.(1, 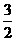 ) 15.(
) 15.(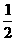 , 1)∪(1, 2)
16.2lg2
, 1)∪(1, 2)
16.2lg2
22.已知数集序列{1}, {3, 5}, {7, 9,11}, {13, 15, 17, 19},……,其中第n个集合有n个元素,每一个集合都由连续正奇数组成,并且每一个集合中的最大数与后一个集合最小数是连续奇数,(1) 求第n个集合中最小数an的表达式;
(2)求第n个集合中各数之和Sn的表达式;
(3)令f(n)=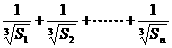 (n≥2),求证:f(2n-1)<n;
(n≥2),求证:f(2n-1)<n;
(4)求证:f(2n)≥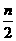 +1.(n≥2)
+1.(n≥2)
21.已知c>0且c≠1,数列{an}是首项为c,公比也为c的等比数列,bn=anlog4an(n∈N), 若数列{bn}中存在最小自然数n,使当m>n且m∈N时,恒有bn>bm,求c的取值范围和相应的n.
20.已知函数f(x)=logb(x+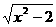 )的反函数为f -1(x),其中b>0,且b≠1,
)的反函数为f -1(x),其中b>0,且b≠1,
(1) 求f -1(x)的解析式及其定义域;(2) 设g(n)=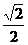 f -1(n+logb
f -1(n+logb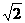 ),若g(n)<
),若g(n)<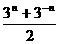 (n∈N),求b的取值范围。
(n∈N),求b的取值范围。
19.已知n∈N, x∈[0, 1],判断1+x+x2+……+xn与n+xn+1的大小,并证明你的结论。
18.已知f(x)=loga(1+x) (a>1),对任意x1, x2∈R+,求证: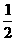 [f(x1-1)+f(x2-1)]≤
[f(x1-1)+f(x2-1)]≤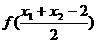 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com