等差、等比数列是数列中的基础，若能转化成一个等差、等比数列问题，则可以利用等差、等比数列的有关性质求解。

例1、流行性感冒(简称流感)是由流感病毒引起的急性呼吸道传染病。某市去年11月份曾发生流感，据资料记载，11月1日，该市新的流感病毒感染者有20人，以后，每天的新感染者平均比前一天的新感染者增加50人。由于该市医疗部门采取措施，使该种病毒的传播得到控制，从某天起，每天的新感染者平均比前一天的新感染者减少30人，到11月30日止，该市在这30天内感染该病毒的患者共有8670人，问11月几日，该市感染此病毒的新患者人数最多？并求这一天的新患者人数。

分析：设11月n日这一天新感染者最多，则由题意可知从11月1日到n日，每天新感染者人数构成一等差数列；从n+1日到30日，每天新感染者构成另一个等差数列。这两个等差数列的和即为这个月总的感染人数。

略解：由题意，11月1日到n日，每天新感染者人数构成一等差数列a_n，a₁=20,d₁=50,11月n日新感染者人数a_n=50n-30；从n+1日到30日，每天新感染者人数构成等差数列b_n,b₁=50n-60,d₂=-30，b_n=(50n-60)+(n-1)(-30)=20n-30­­,11月30日新感染者人数为b_30-n=20(30-n)-30=-20n+570.

故共感染者人数为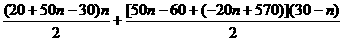：=8670，化简得：n²-61n+588=0,解得n=12或n=49(舍)，即11月12日这一天感染者人数最多，为570人。

22．(14分)已知函数f(x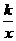)=x+,其中x.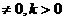

(1)判断f(x)的奇偶性；

(2)判断当x>0时，f(x)的单调性，并证明之；

(3)若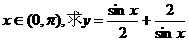的最小值.

21．(12分)假设国家收购某种农产品的价格是120元/担，其中征税标准为每100元征8元(叫税率为8%)，计划可收购m万担(其中m为正常数)，为了减轻农民负担，如果税率降低x%，预计收购量可增加(2x)%.

　　　 (1)写出税收y(万元)与x的函数关系式；

　　　 (2)要使此项税收在税率调节后不低于原计划的78%，求x取值范围.

20．(12分)解关于x的不等式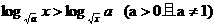

19．(12分)已知△ABC中，三内角A、B、C成等差数列，其外接圆半径为1，且有sinA－sinC+.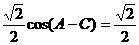

　 　 求：(1)A、B、C的大小　 (2) △ABC的面积.

18．(12分)已知函数y=lg(x²+2x+a)

　　　 (1)若函数定义域为R，求a的取值范围；

　　　 (2)若函数的值域为R，求a的取值范围；

　　　 (3)若函数的值域为[0，+∞]，求a的取值范围.

17．(12分)(1)已知tgα=3,求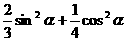：的值。

　 (2)已知tgα+sinα=m, tgα-sinα=n (,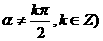

求证：.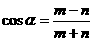

16．给出下列四个命题，①若f(x+2)=f(2－x),则f(x)的图象关于x=2对称，②若f(x+2)=f(2－x),则f(x)的图象关于y轴对称。③函数y=f(2+x)与y=f(2－x)的图象关于x=2对称。④函数y=f(2+x)与y=f(2-x)的图象关于y轴对称。正确的命题是　　　　 .

15．设f(x)=4^x－2^x+1 (x>0),则=　　　　　　　　 .

14．已知sinx+cosx =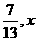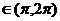,则tgx =　　　　　　 .