
题目列表(包括答案和解析)
4.设椭圆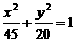 的两个焦点为F1、F2,P为椭圆上一点,且PF1⊥PF2,则||PF1|-|PF2||=_________.
的两个焦点为F1、F2,P为椭圆上一点,且PF1⊥PF2,则||PF1|-|PF2||=_________.
3.已知圆x2+y2=4,又Q(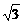 ,0),P为圆上任一点,则PQ的中垂线与OP之交点M轨迹为(O为原点)
,0),P为圆上任一点,则PQ的中垂线与OP之交点M轨迹为(O为原点)
A.直线 B.圆 C.椭圆 D.双曲线
2.若方程x2+ky2=2,表示焦点在y轴上的椭圆,那么实数k的取值范围是
A.(0,+∞) B.(0,2)
C.(1,+∞) D.(0,1)
1.椭圆中心在坐标原点,对称轴为坐标轴,离心率为0.6,长、短轴之和为36,则椭圆方程为
A.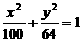
B.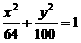
C.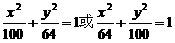
D.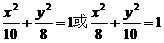
10. 翰林汇0已知双曲线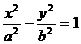 的离心率
的离心率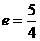 , 半虚轴长为2, 求双曲线方程.
, 半虚轴长为2, 求双曲线方程.
解:∵
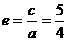 , 可令a=4k, c=5k, 则b2=c2-a2=9k2=4,
, 可令a=4k, c=5k, 则b2=c2-a2=9k2=4,
∴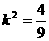 .于是
.于是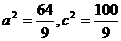 ,
,
故双曲线方程为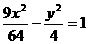 .翰林汇
.翰林汇
9.求双曲线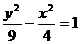 的以点P(a,1)为中点的弦所在直线方程,并讨论a取怎样的值时这样的弦才存在.
的以点P(a,1)为中点的弦所在直线方程,并讨论a取怎样的值时这样的弦才存在.
解:y=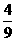 ax-
ax-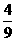 a2+1.只有当-
a2+1.只有当-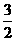 <a<
<a<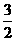 或a>
或a> 或a<-
或a<- 时,
时,
以点P为中点的弦才存在.翰林汇
8.已知P为双曲线3x2-5y2=15上的一点, F1,F2为其两个焦点, 且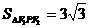 ,求∠F1PF2的大小.
,求∠F1PF2的大小.
解:令∠F1PF2=θ, |PF1|=m,
|PF2|=n, 则由余弦定理可得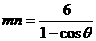 ,
,
又由S△=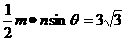 ,
,
于是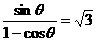 , 最后得
, 最后得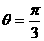 .翰林汇
.翰林汇
7.双曲线中点在原点,准线平行x轴,离心率为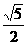 ,若点P(0,5)到双曲线上的点的距离的最小值是2时,求双曲线的方程.翰林汇
,若点P(0,5)到双曲线上的点的距离的最小值是2时,求双曲线的方程.翰林汇
翰林汇解几解解:设双曲线方程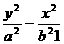 ;M(x,y)为双曲线上任意一点.
;M(x,y)为双曲线上任意一点.
由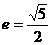 ,∴
,∴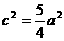 ,∴b2=c2-a2=
,∴b2=c2-a2=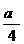 .
.
而|PM|2=x2+(y-5)2=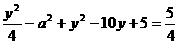 (y-4)2+5-a2.
(y-4)2+5-a2.
以下分a≤4或a>4讨论,
得双曲线方程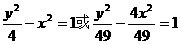
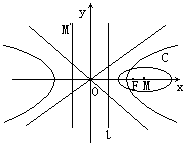
6.已知点F与直线l分别是双曲线x2-3y2=3的右焦点与右准线, 以F为左焦点 , l为左准线的椭圆C的中心为M, 又M关于直线y=2x的对称点M′恰好在已知双曲线的左准线上(如图),
求椭圆C的方程及其离心率.
解:∵ F(2,0) 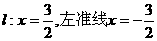 , 再设P(x,y)在C上,
, 再设P(x,y)在C上,
则由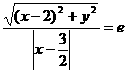 , 得(1-e2)x2+y2+(3e2-4)x+4-
, 得(1-e2)x2+y2+(3e2-4)x+4-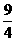 e2=0,
e2=0,
于是中心为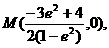
由条件得方程为x2+2y2-5x+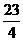 =0,
=0,
即4x2+8y2-20x+23=0, 离心率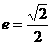
3.点P在双曲线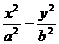 =1上,F1、F2是左右焦点,O为原点,
=1上,F1、F2是左右焦点,O为原点,
求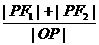 的取值范围.
的取值范围.
解: 设点P(x0,y0)在右支上,离心率为e,
则有|PF1|=ex0+a,|PF2|=ex0-a,|OP|= =1,
=1,
所以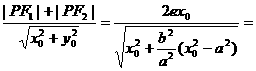
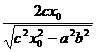 ,
,
设t=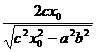 , ∴t2=
, ∴t2=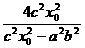 ,解得
,解得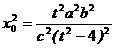
这里t2-4>0,又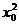 ≥a2,
≥a2,
∴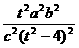 ≥a2 ∴
≥a2 ∴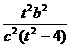 ≥1 ∴
≥1 ∴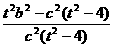 ≥0,由此得:
≥0,由此得:
 解得2<t≤2e
解得2<t≤2e
当点P在左支上时,同理可以得出此结论.翰林汇翰林汇
翰林汇4.已知直线y=x+b与双曲线2x2-y2=2相交于A, B两点, 若以AB为直径的圆过原点,
求b的值翰林汇。翰林汇
解:翰林汇 设A(x1,y1), B(x2,y2), 则 由条件可得:
x1+x2=2b, x1x2=-b2-2, y1y2=-x1x2,
最后得b=±2.翰林汇
翰林汇5.已知双曲线的中心在原点,对称轴为坐标轴,离心率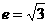 ,一条准线的方程为
,一条准线的方程为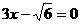 ,求此双曲线的标准方程.
,求此双曲线的标准方程.
解:
由题设,  解得
解得 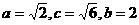 .
.
∴双曲线方程为
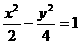 .翰林汇
.翰林汇
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com