
题目列表(包括答案和解析)
2.一双曲线以y轴为右准线,其右支过点M(1,2),且它的虚轴长、实轴长、焦距顺次成等差数列,试求:
(1)双曲线右焦点F的轨迹方程;(2)实轴最长的双曲线方程;
(3)过点M、F的弦的另一端点N的轨迹方程(不必求出轨迹范围).
解:(1)(x-1)2+(y-2)2=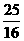 (x>0);
(x>0);
(2)9(x+4)2-16(y-2)2=225;
(3)9x2-16y2+82x+64y-55=0.翰林汇翰林汇
1. 已知双曲线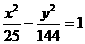 的左右焦点分别为F1、F2,左准线为L,能否在双曲线的左支上求一点P,使|PF1|是P到L的距离d与|PF2|的等比中项?若能,求出P点坐标,若不能,说明理由。
的左右焦点分别为F1、F2,左准线为L,能否在双曲线的左支上求一点P,使|PF1|是P到L的距离d与|PF2|的等比中项?若能,求出P点坐标,若不能,说明理由。
解:假定在左支上存在一点P适合题意,
则有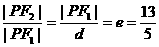 ,
,
∴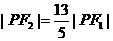 ,又|PF2|-|PF1| = 10,
,又|PF2|-|PF1| = 10,
∴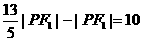 ,
,
∴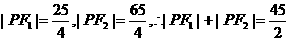 ,
,
又由于|PF1|+|PF2|≥|F1F2| = 26,上两式矛盾,
∴P不存在.翰林汇
8.(2002年全国高考题)设点P到点M(-1,0)、N(1,0)距离之差为2m,到x轴、y轴距离之比为2.求m的取值范围.
7.在双曲线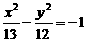 的一支上有不同三点A(x1,y1)、B(x2,6)、C(x3,y3)与点F(0,5)的距离|AF|、|BF|、|CF|依次成等差数列,
的一支上有不同三点A(x1,y1)、B(x2,6)、C(x3,y3)与点F(0,5)的距离|AF|、|BF|、|CF|依次成等差数列,
(1)求y1+y2的值;
(2)求证线段AC的垂直平分线经过一定点,求出定点的坐标.
6.如图,OA是双曲线的实半轴,OB是虚半轴,F为焦点,且∠BAO=30°,S△ABF=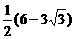 ,求该双曲线的方程.
,求该双曲线的方程.
5.设F1、F2是双曲线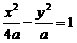 (a>0)的两个焦点,P在双曲线上,∠F1PF2=90°,若Rt△F1PF2的面积是1,则a的值是_________.
(a>0)的两个焦点,P在双曲线上,∠F1PF2=90°,若Rt△F1PF2的面积是1,则a的值是_________.
4.已知双曲线渐近线方程为y=±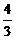 x,且焦点都在圆x2+y2=100上,则双曲线方程为_________.
x,且焦点都在圆x2+y2=100上,则双曲线方程为_________.
3.如果方程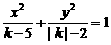 表示双曲线,则k的取值范围是
表示双曲线,则k的取值范围是
A.|k|>2 B.|k|<2
C.k>5或|k|<2 D.2<k<5或k<-2
2.若双曲线的两条渐近线是y=±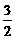 x,焦点F1(-
x,焦点F1(- ,0)、F2(
,0)、F2( ,0),那么它的
,0),那么它的
两条准线间的距离是
A.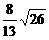 B.
B.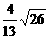
C.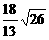 D.
D.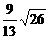
1.(2002年全国高考题)设θ∈(0,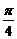 ),则二次曲线x2cotθ-y2tanθ=1的离心率的取值范围为
),则二次曲线x2cotθ-y2tanθ=1的离心率的取值范围为
A.(0,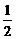 ) B.(
) B.(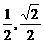 )
)
C.(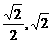 ) D.(
) D.(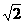 ,+∞)
,+∞)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com