
题目列表(包括答案和解析)
11 (文)命题“若
(文)命题“若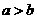 ,则
,则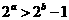 ”的否命题为
”的否命题为

(理)如果椭圆的对称轴为坐标轴,短轴的一个端点与两焦点组成一正三角形,焦点在y轴上,且a-c=,
那么椭圆的方程是

12 (文)
(文)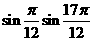 的值是
的值是

(理)函数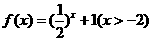 的反函数
的反函数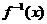 是
是
13 (文)如果椭圆的对称轴为坐标轴,短轴的一个端点与两焦点组成一正三角形,焦点在y轴上,且a-c=,
那么椭圆的方程是
(文)如果椭圆的对称轴为坐标轴,短轴的一个端点与两焦点组成一正三角形,焦点在y轴上,且a-c=,
那么椭圆的方程是 
(理)已知直线ax+by+c=0被圆M: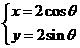 所截得的弦AB的长为
所截得的弦AB的长为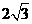 ,那么
,那么
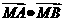 的值等于
的值等于

14 已知直线ax+by+c=0被圆M:
已知直线ax+by+c=0被圆M: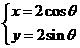 所截得的弦AB的长为
所截得的弦AB的长为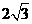 ,那么
,那么
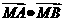 的值等于
的值等于

15 已知函数
已知函数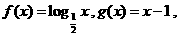 设
设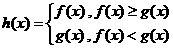 ,则使
,则使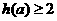 成立的
成立的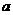 的范围是
的范围是

16 有 以下几个命题
有 以下几个命题
①曲线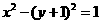 按
按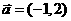 平移可得曲线
平移可得曲线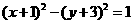 ;
;
②若|x|+|y|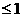 ,则使x+y取得最大值和最小值的最优解都有无数多个;
,则使x+y取得最大值和最小值的最优解都有无数多个;
③设A、B为两个定点,为常数 ,
,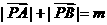 ,则动点P的轨迹为椭圆;
,则动点P的轨迹为椭圆;
④若椭圆的左、右焦点分别为F1、F2,P是该椭圆上的任意一点,则点F2关于“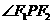 的外角平分线”的对称点M的轨迹是圆
的外角平分线”的对称点M的轨迹是圆
其中真命题的序号为
;(写出所有真命题的序号)
1 设集合P={直线的倾斜角},Q={两个向量的夹角},R={两条直线的夹角},M={直线l1到l2的角}则必有
设集合P={直线的倾斜角},Q={两个向量的夹角},R={两条直线的夹角},M={直线l1到l2的角}则必有
A Q
Q R=P
R=P M
B
M
B R
R M
M P
P Q
Q
C Q=R
Q=R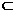 M=P
D
M=P
D R
R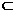 P
P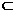 M
M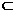 Q
Q
2 在等差数列
在等差数列 中,若
中,若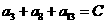 ,则其前n项和
,则其前n项和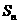 的值等于5C的是
的值等于5C的是
A
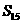 B
B
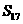 C
C
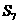 D
D
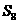
3 (文)若点B分
(文)若点B分 的比为
的比为 ,且有
,且有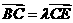 ,则
,则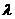 等于
等于
A 2
B
2
B
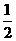 C
C 1
D
1
D -1
-1
(理)函数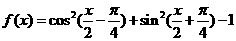 是
是
A 周期为
周期为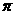 的奇函数
B
的奇函数
B 周期为
周期为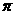 的偶函数
的偶函数
C 周期为
周期为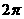 的奇函数
D
的奇函数
D 周期为
周期为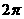 的偶函数
的偶函数
4 过点(-4,0)作直线L与圆x2+y2+2x-4y-20=0交于A、B两点,如果|AB|=8,
过点(-4,0)作直线L与圆x2+y2+2x-4y-20=0交于A、B两点,如果|AB|=8,
则L的方程为
A 5x+12y+20=0
B
5x+12y+20=0
B 5x-12y+20=0
5x-12y+20=0
C 5x-12y+20=0或x+4=0
D
5x-12y+20=0或x+4=0
D 5x+12y+20=0或x+4=0
5x+12y+20=0或x+4=0
5 (文)已知p,
q, p+q是等差数列,p ,q ,pq是等比数列,则椭圆
(文)已知p,
q, p+q是等差数列,p ,q ,pq是等比数列,则椭圆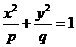 的准线方程是
的准线方程是
A
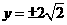 B
B
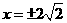 C
C
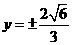 D
D
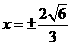
(理)已知命题P:关于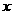 的不等式
的不等式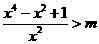 的解集为
的解集为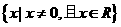 ;命题Q:
;命题Q: 是减函数
是减函数 若P或Q为真命题,P且Q为假命题,则实数
若P或Q为真命题,P且Q为假命题,则实数 的取值范围是
的取值范围是
A (1,2)
B
(1,2)
B
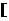 1,2)
C
1,2)
C (-
(- ,1
,1 D
D (-
(- ,1)
,1)
6 (文)已知命题P:关于
(文)已知命题P:关于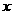 的不等式
的不等式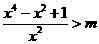 的解集为
的解集为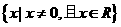 ;命题Q:
;命题Q: 是减函数
是减函数 若P或Q为真命题,P且Q为假命题,则实数
若P或Q为真命题,P且Q为假命题,则实数 的取值范围是
的取值范围是
A (1,2)
B
(1,2)
B
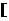 1,2)
C
1,2)
C (-
(- ,1
,1 D
D (-
(- ,1)
,1)
(理)若点B分 的比为
的比为 ,且有
,且有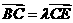 ,则
,则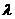 等于
等于
A 2
B
2
B
 C
C 1
D
1
D -1
-1
7 (文)函数
(文)函数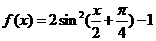 是
是
A 周期为
周期为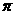 的奇函数
B
的奇函数
B 周期为
周期为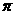 的偶函数
的偶函数
C 周期为
周期为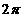 的奇函数
D
的奇函数
D 周期为
周期为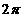 的偶函数
的偶函数
(理)若 ,对任意实数
,对任意实数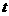 都有
都有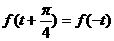 ,且
,且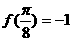 , 则实数
, 则实数 的值等于
的值等于
A
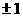 B
B
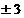 C
C -3或1 D
-3或1 D -1或3
-1或3
8 (文)若
(文)若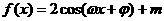 ,对任意实数
,对任意实数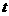 都有
都有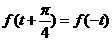 ,且
,且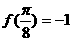 , 则实数
, 则实数 的值等于
的值等于
A
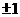 B
B
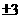 C
C -3或1 D
-3或1 D -1或3
-1或3
(理)设函数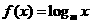 ,数列
,数列 是公比为
是公比为 的等比数列,若
的等比数列,若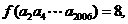 则
则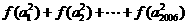 的值等于
的值等于
A -1974
B
-1974
B -1990
C
-1990
C 2022
D
2022
D 2038
2038
9 (文)设函数
(文)设函数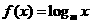 ,数列
,数列 是公比为
是公比为 的等比数列,若
的等比数列,若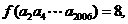 则
则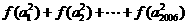 的值等于
的值等于
A -1974
B
-1974
B -1990
C
-1990
C 2022
D
2022
D 2038
2038
(理)函数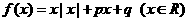 是奇函数,且在R上是增函数的充要条件是
是奇函数,且在R上是增函数的充要条件是
A p>0 ,q=0
B
p>0 ,q=0
B p<0 ,q=0 C
p<0 ,q=0 C p≤0,q=0 D
p≤0,q=0 D p≥0,q=0
p≥0,q=0
10 (文)函数
(文)函数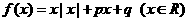 是奇函数,且在R上是增函数的充要条件是
是奇函数,且在R上是增函数的充要条件是
A p>0 ,q=0
B
p>0 ,q=0
B p<0 ,q=0 C
p<0 ,q=0 C p≤0,q=0 D
p≤0,q=0 D p≥0,q=0
p≥0,q=0
(理)已知函数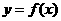 满足:①
满足:①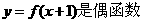 ;②在
;②在 上为增函数
上为增函数
若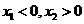 ,且
,且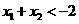 ,则
,则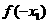 与
与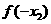 的大小关系是
的大小关系是
A
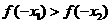 B
B
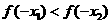
C
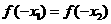 D
D 无法确定
无法确定
第Ⅱ卷 (非选择题,共100分)
1 第Ⅱ共6页,用蓝、黑色的钢笔或圆珠笔直接答在试卷中
第Ⅱ共6页,用蓝、黑色的钢笔或圆珠笔直接答在试卷中
2 答卷前,请将密封线内的项目填写清楚
答卷前,请将密封线内的项目填写清楚
21、(I)当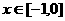 时,
时,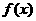 上的点P(
上的点P(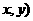 与
与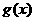 上的点Q(
上的点Q(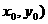
关于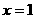 对称,则
对称,则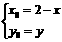 此时
此时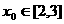 代入
代入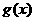
得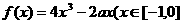 )
)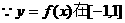 上是偶函数
上是偶函数
 当
当 时,
时,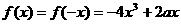
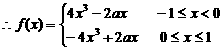 ………………………………5分
………………………………5分
(II)命题条件等价于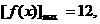 因为
因为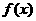 为偶函数,所以只需考虑
为偶函数,所以只需考虑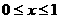 的情况.
的情况.
求导
由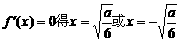 (舍)…………………………8分
(舍)…………………………8分
①当0<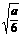 <1,即
<1,即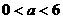 时
时
 |
0 |
(0,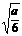 ) ) |
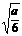 |
(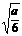 ,1) ,1) |
1 |
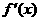 |
|
+ |
|
- |
|
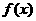 |
0 |
 |
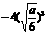 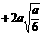 |
 |
-4+2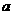 |
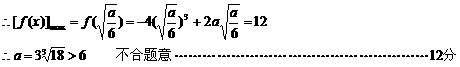
②当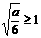 ,即
,即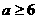 时,
时,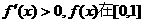 上单调递增
上单调递增

综上,存在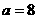 使得
使得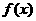 的图象的最高点在直线
的图象的最高点在直线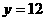 上.……………14分
上.……………14分
21. (本小题满分14分)
设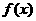 是定义在[-1,1]上的偶函数,
是定义在[-1,1]上的偶函数,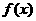 ,
,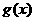 的图象关于直线
的图象关于直线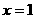 对称,且当
对称,且当
x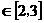 时,
时,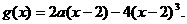
(1)求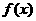 的表达式;
的表达式;
(2)是否存在正实数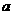 ,使函数
,使函数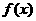 的图象的最高点在直线
的图象的最高点在直线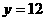 上,若存在,求出正实数
上,若存在,求出正实数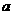 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
20. (本小题满分14分)
函数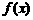 的定义域为R,并满足以下条件:
的定义域为R,并满足以下条件:
①对任意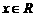 ,有
,有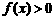 ;
;
②对任意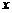 、
、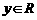 ,有
,有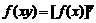 ;
;
③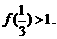
(Ⅰ)求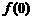 的值;
的值;
(Ⅱ)求证: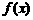 在R上是单调增函数;
在R上是单调增函数;
(Ⅲ)若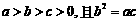 ,求证:
,求证: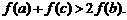
解法一:(1)令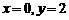 ,得:
,得: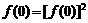

(2)任取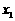 、
、 ,且
,且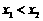 .设
.设 则
则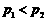
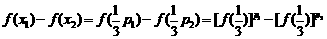
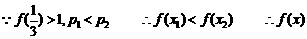 在R上是单调增函数
在R上是单调增函数
(3)由(1)(2)知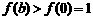
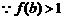
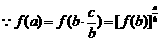
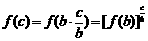
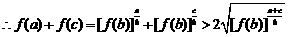
而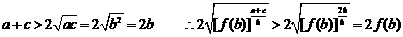
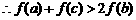
解法二:(1)∵对任意x、y∈R,有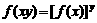
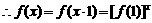
∴当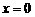 时
时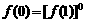
∵任意x∈R, 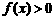
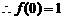
(2)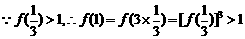
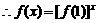 是R上单调增函数
即
是R上单调增函数
即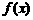 是R上单调增函数;
是R上单调增函数;
(3)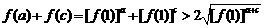
而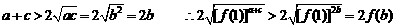
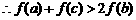
19. (本小题满分14分)
已知f (x)=x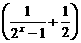 ,
,
(1) 证明:f (x)>0;
(2) 设F(x)=f(x+t)-f (x-t) (t≠o),试判断F(x)的奇偶性。
解:(1) 函数f (x)的定义域是{x| x∈R且x≠0}, 且f (-x)=(-x)· =f (x),
=f (x),
∴ f (x)是偶函数。当x>0时, 2x>1, 2x-1>0, ∴ f (x)>0,
当x<0时, -x>0, f (x)=f (-x)>0, ∴ 对所有定义域内的x的值,都有f (x)>0.
(2) F(-x)=f (-x+t)-f (-x-t)=f (x-t)-f (x+t)=-F(x), ∴ 函数是奇函数。
18. (本小题满分14分)
统计表明,某种型号的汽车在匀速行驶中每小时耗油量y(升)关于行驶速度x(千米/小时)的函数解析式可以表示为:y=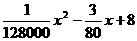 (0<x≤120).已知甲、乙两地相距100千米。
(0<x≤120).已知甲、乙两地相距100千米。
(Ⅰ)当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地要耗油多少升?
(Ⅱ)当汽车以多大的速度匀速行驶时,从甲地到乙地耗油最少?最少为多少升?
解:(I)当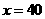 时,汽车从甲地到乙地行驶了
时,汽车从甲地到乙地行驶了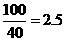 小时,
小时,
要耗没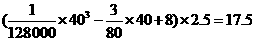 (升)。
(升)。
答:当汽车以40千米/小时的速度匀速行驶时,从甲地到乙地耗油17.5升。
(II)当速度为 千米/小时时,汽车从甲地到乙地行驶了
千米/小时时,汽车从甲地到乙地行驶了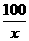 小时,设耗油量为
小时,设耗油量为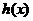 升,
升,
依题意得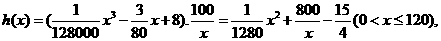
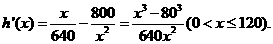
令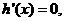 得
得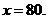
当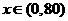 时,
时,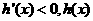 是减函数;
是减函数;
当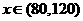 时,
时,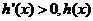 是增函数。
是增函数。
 当
当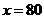 时,
时,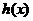 取到极小值
取到极小值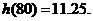
因为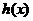 在
在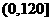 上只有一个极值,所以它是最小值。
上只有一个极值,所以它是最小值。
答:当汽车以80千米/小时的速度匀速行驶时,从甲地到乙地耗油最少,最少为11.25升。
17.(本小题满分12分)
若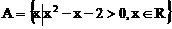 ,
,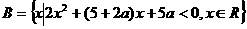 ,
,
且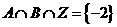 ,其中Z为整数集,求实数
,其中Z为整数集,求实数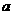 的取值范围。
的取值范围。
解:.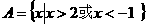 ,
,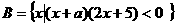 (………………2分)
(………………2分)
(1)当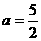 时,
时,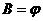 不符合题意.(…………………5分)
不符合题意.(…………………5分)
(2)当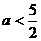 时,
时, 得
得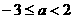 (……………………9分)
(……………………9分)
(3)当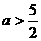 时,
时,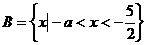 不符合题意。(…………………12分)
不符合题意。(…………………12分)
综上所得 (…………………14)
(…………………14)
16.(本题满分12分)
解:(1)1,37 (2)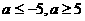
16.(本小题满分12分)
已知函数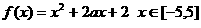
(1)当a=-1时,求函数f (x)的最大值和最小值.
(2)求实数a的取值范围,使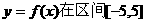 上是单调函数.
上是单调函数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com