
题目列表(包括答案和解析)
22.(14分)已知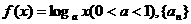 ,若数列{an}
,若数列{an}
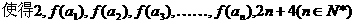 成等差数列.
成等差数列.
(1)求{an}的通项an;
(2)设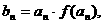 若{bn}的前n项和是Sn,且
若{bn}的前n项和是Sn,且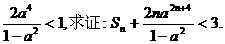
21.(12分)椭圆C1: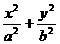 =1(a>b>0)的左右顶点分别为A、B.点P双曲线C2:
=1(a>b>0)的左右顶点分别为A、B.点P双曲线C2: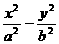 =1在第一象限内的图象上一点,直线AP、BP与椭圆C1分别交于C、D点.若△ACD与△PCD的面积相等.
=1在第一象限内的图象上一点,直线AP、BP与椭圆C1分别交于C、D点.若△ACD与△PCD的面积相等.
(1)求P点的坐标;
(2)能否使直线CD过椭圆C1的右焦点,若能,求出此时双曲线C2的离心率,若不能,请说明理由.
20.(12分)某集团准备兴办一所中学,投资1200万用于硬件建设.为了考虑社会效益和经济利益,对该地区教育市场进行调查,得出一组数据列表(以班为单位)如下:
|
|
班级学生数 |
配备教师数 |
硬件建设(万元) |
教师年薪(万元/人) |
|
初中 |
60 |
2.0 |
28 |
1.2 |
|
高中 |
40 |
2.5 |
58 |
1.6 |
根据有关规定,除书本费、办公费外,初中生每年可收取学费600元,高中生每年可收取学费1500元.因生源和环境等条件限制,办学规模以20至30个班为宜.根据以上情况,请你合理规划办学规模使年利润最大,最大利润多少万元?
(利润=学费收入-年薪支出)
19.(12分)定义在R上的函数f(x)满足f(x+2)=-f(x),且当x∈[-1,1]时,f(x)=x3.
(1)求f(x)在[1,5]上的表达式;
(2)若A={x|
f(x)>a,x∈R},且A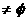 ,求实数a的取值范围.
,求实数a的取值范围.
18.(12分)(1)已知|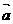 |=4,|
|=4,|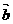 |=3,(2
|=3,(2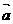 -3
-3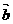 )·(2
)·(2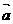 +
+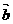 )=61,求
)=61,求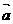 与
与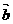 的夹角θ;
的夹角θ;
(2)设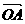 =(2,5),
=(2,5), =(3,1),
=(3,1),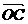 =(6,3),在
=(6,3),在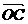 上是否存在点M,使
上是否存在点M,使
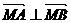 ,若存在,求出点M的坐标,若不存在,请说明理由.
,若存在,求出点M的坐标,若不存在,请说明理由.
17.(12分)已知函数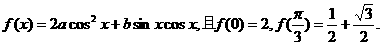
(1)求f(x)的最大值与最小值;
(2)若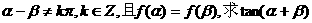 的值.
的值.
16.奇函数f(x)的定义域为 值域为R,当且仅当x>1时,f(x)>0.关于f(x)有如下命题:①f(-1)=0;②方程f(x)=0有无穷解;③f(x)有最小值,但无最大值;④f(x)的图象关于原点对称,且f(x)是周期函数.其中正确命题的序号是
.
值域为R,当且仅当x>1时,f(x)>0.关于f(x)有如下命题:①f(-1)=0;②方程f(x)=0有无穷解;③f(x)有最小值,但无最大值;④f(x)的图象关于原点对称,且f(x)是周期函数.其中正确命题的序号是
.
15.当x=3时,不等式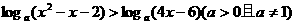 成立,则此不等式的解集是
.
成立,则此不等式的解集是
.
14.把点A(2,1)按向量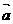 =(-2,3)平移到B,此时点B分向量
=(-2,3)平移到B,此时点B分向量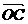 (O为坐标原点)的比为-2,则C点的坐标为
.
(O为坐标原点)的比为-2,则C点的坐标为
.
13.△ABC中,若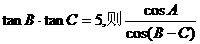 的值为
.
的值为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com