19．已知在四棱锥P-ABCD中，底面ABCD是直角梯形，∠BAD = 90°，2AB=2AD=CD，侧面PAD是正三角形且垂直于底面ABCD，E是PC上一点.

　 (1)点E是PC中点时，求证：BE⊥平面PCD；

　 (2)在(1)的条件下，求二面角C-BD-E的大小；

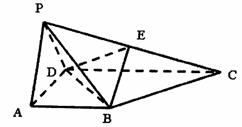　 　 (3)当E是PC中点时，在PB上是否存在一点F，使AF∥平面BDE.若存在，请确定点F的位置；若不存在，请说明理由.

18．(1)求值：；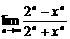

　 (2)令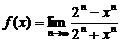，画出函数f (x)的图象并判断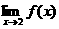是否存在，说明理由.

17．某射手进行射击训练，假设每次射击击中目标的概率为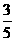，且各次射击的结果互不影响.

　 (1)求射手在3次射击中，至少有两次连续击中目标的概率；

　 (2)求射手第3次击中目标时，恰好射击了4次的概率；

　 (3)设随机变量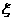表示射手第3次击中目标时已射击的次数，求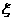的分布列.

16．求函数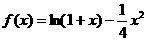在[0，2]上的最大值与最小值.

15．已知函数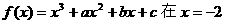处取得极值，并且它的图象与直线

y =－3x + 3在点(1，0)处相切，求a、b、c的值.

14．四面体ABCD中，(1)若AC⊥BD，AB⊥CD，则AD⊥BC；(2)若E、F、G分别是BC、AB、CD中点，则∠FEG的大小等于直线AC、BD所成角大小；(3)若O为四面全ABCD外接球球心，则O在面ABD上的射影是△ABD的外心；(4)若四个面是全等三角形，则ABCD是正四面体。其中正确的命题是　　　　　　　　 。

13．设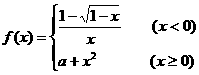，要使f (x)在x = 0处连续，则实数a的值为　　　 ；

12．已知过球面上三点A、B、C的截面到球心的距离等于球的半径的一半，且AC=BC=6，AB = 4，则球的表面积为　　　　　　 ；

11．某工厂生产A、B、C三种不同型号的产品，产品数量之比依次为2 ：3 ：4，现用分层抽样方法抽出一个容量为n的样本，样本中A种型号的产品有16件，则n = 　　　　；

10．如果四棱锥的四条侧棱都相等，就称它为“等腰四棱锥”，四条侧棱称为它的腰，以下4个命题中，假命题是　　　　 　　　　　　　　　　　　　　　　 (　　 )

　　　 A．等腰四棱锥的腰与底面所成的角都相等

　　　 B．等腰四棱锥的侧面与底面所成的二面角都相等或互补

　　　 C．等腰四棱锥的底面四边形必存在外接圆

　　　 D．等腰四棱锥的各顶点必在同一球面上