
题目列表(包括答案和解析)
3、设点P为曲线y=x3-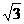 x +
x +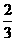 上的任意一点,P点处切线倾斜角为α,则α的取值范围为( )
上的任意一点,P点处切线倾斜角为α,则α的取值范围为( )
A、[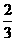 π,π] B、(
π,π] B、(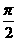 ,π) C、[0,
,π) C、[0,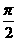 ]∪(
]∪(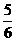 π,π)
π,π)
D、[0,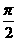 ]∪[
]∪[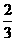 π,π)
π,π)
2、若y=f (x)的定义域为D,且为单调函数,[a,b]D,(a-b)·f (a)·f (b)>0,则下列命题正确为( )
A、若f (x)=0,则x∈(a,b) B、若f (x)>0,则x  (a,b)
(a,b)
C、若x∈(a,b),则f (x)=0 D、若f (x)<0,则x  (a,b)
(a,b)
1、定义域为R的函数y=f (x)的值域为[a,b],则函数y=f (x+a)的值域为( )
A、[2a,a+b] B、[a,b] C、[0,b-a] D、[-a,a+b]
22.(本小题满分12分)
设a∈R,函数f(x)=(ax2-2x)e-x.
(1)当a≥0时,求f (x)的极值点;
(2)设f(x)在[-1,1]上是单调函数,求a的取值范围.




21.(本小题满分12分)
已知数列{an}中a1= , an=2-
, an=2-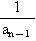 (n≥2),设bn=
(n≥2),设bn=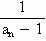
(1)求数列{an}的通项公式;
(2)记sn=b1+b2+…+bn,求 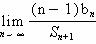 .
.
20.(本小题满分12分)
甲、乙两人掷硬币,甲用一枚硬币掷3次,记正面朝上的次数为ξ;乙用这枚硬币掷2次,记正面朝上的次数为η.
(1)求Eξ和Dξ;
(2)规定:若ξ>η,则甲获胜;若ξ<η,则乙获胜,分别求出甲、乙获胜的概率.
19.(本小题满分12分)
已知椭圆的中心在原点,离心率为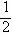 ,一个焦点是F(-1,0).
,一个焦点是F(-1,0).
(1)求随圆的方程;
(2)设Q是椭圆上的一点,且过点F、Q的直线l与y轴交于点M,若|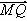 |=2|
|=2|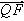 |,求直线l的斜率.
|,求直线l的斜率.
18.(本小题满分12分)
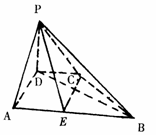 在四棱锥P-ABCD中,PD⊥底面ABCD,AB∥CD,PD=CD=AD=
在四棱锥P-ABCD中,PD⊥底面ABCD,AB∥CD,PD=CD=AD=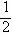 AB,∠ADC
AB,∠ADC
=120°.
(1)求证:平面APD⊥平面PDB;
(2)若AB的中点为E,求二面角D-PC-E的大小.
17.(本小题满分10分)已知点A(4,0),B(0,4),C(3cosα,3sinα).
(1)若α∈(-π,0),且|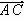 |=|
|=| |,求角α的值;
|,求角α的值;
(2)若
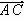 ·
· =0,求
=0,求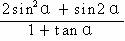 的值.
的值.
16.给出下列四个命题:
①函数y=f(x)在x=x0处可导,则函数y=f(x)在x0处连续;
②函数y=f(x)在x=x0处的导数f (x0)=0,则f(x0)是函数y=f(x)的一个极值;
③函数y=f(x)在x=x0处的导数不存在,则f(x0)不是函数y=f(x)的一个极值;
④函数y=f(x)在x=x0处的导数不存在,则f(x0)不是函数y=f(x)的最值.
其中正确的命题的序号是________________(请把所有正确命题的序号都填上).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com