33、设函数f (x)的定义域为(0，+∞)且对任意正实数x、y有f (xy)＝f (x)+f (y)。已知f (2)＝1，且当x＞1时，f (x)＞0。

　(1)判断f (x)在(0，+∞)上的单调性。

　(2)正数数列{an}的前n项和为Sn，且满足f (S n)＝f (a n)+f (a n+1)－1(n∈N^＊)，求{a n}的通项公式。

32、已知f (x)＝为奇函数，f (1)＜f (3)，且不等式0≤ f (x)≤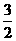的解集是［－2，－1］∪　［2,4］。(1)求a、b、c的值；(2)是否存在实数m使不等式f (－2+sinθ)＜－m²+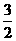对一切θ∈R成立？若存在，求出m的取值范围。若不存在，请说明理由。

31、已知f (x)是定义在［－1,1］上的奇函数，且f (1)＝1，若a、b∈［－1,1］，a+b≠0，有

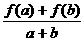＞0。

　⑴判断f (x)在［－1,1］上是增函数还是减函数，并证明你的结论；

　⑵解不等式f (x+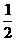)＜f ( 　)；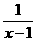

　⑶若f (x)≤m²－2am+1对所有x∈［－1,1］，a∈［－1,1］恒成立，求实数m的范围。

30、(理)设f (x)＝(x+1)ln(x+1)，若对所有的x≥0，都有f (x)≥ax成立，求实数a的取值范围。

29、对于正整数n和m，其中m＜n，定义n m！＝(n－m)(n－2m)…(n－km)，其中k是满足　n＞km的最大整数，则＝　　　　　。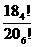

28、已知x∈R，［x］表示不大于x的最大整数，如［π］＝3，［－1,2］＝－2，则使　　　　　　　　 ［｜x²－1｜］＝3成立的x取值范围为　　　　　。

27、在锐角△ABC中，tamA，tanB是方程x²+mx+m+1＝0的两根，则m∈ 　　　　　　　　　　　　　。

26、对任意实数x、y定义运算x*y＝ax+by+cxy，其中a、b、c为常数，等号右边的运算是通常意义的加、乘运算，现已知1＊2＝3,2＊3＝4，且有一个非零常数m，使得对任意实数x，都有　

x＊m＝x，则m＝　　　　　　。

25、已知函数f(3x+2)的定义域为(－2,1)，则f (1－2x)的定义域为　　　　　。

24、已知定义在R上的偶函数f (x)，满足f (x+2)＊f (x)＝1，对x∈R恒成立，且f (x)＞0，则　　f (119)＝　　　　。