
题目列表(包括答案和解析)
4、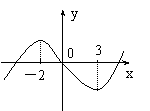 函数
函数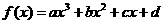 图象如右图,则函数
图象如右图,则函数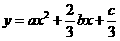 的单调递增区间为( )
的单调递增区间为( )
A、 B、
B、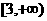
C、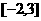 D、
D、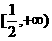
3、已知曲线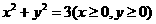 与函数
与函数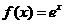 和
和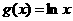 分别交于
分别交于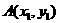 ,
,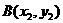 两点,则
两点,则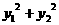 的值为( )
的值为( )
A、1 B、2 C、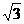 D、3
D、3
2、已知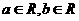 ,且ab<0,则
,且ab<0,则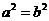 是复数
是复数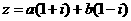 为纯虚数的( )
为纯虚数的( )
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、既不充分也不必要条件
1、定义集合M与N的新运算,M+N=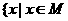 或
或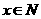 且
且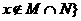 ,则(M+N)+N等于( )
,则(M+N)+N等于( )
A、 B、
B、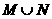 C、M D、N
C、M D、N
20、(14分)已知定义域为R的二次函数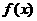 的最小值为0且有
的最小值为0且有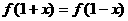 ,直线
,直线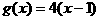 被
被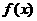 的图像截得的弦长为
的图像截得的弦长为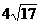 ,数列
,数列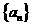 满足
满足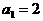 ,
,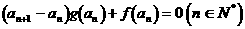 .
.
(1)求函数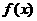 ;
;
(2)求数列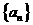 的通项公式;
的通项公式;
(3)设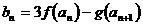 ,求数列
,求数列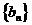 的最值及相应的n。
的最值及相应的n。
(1)解:设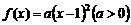 ,则直线
,则直线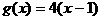 与
与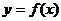 图象的两个交点为(1,0),
图象的两个交点为(1,0),
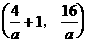 ………………………2分
………………………2分
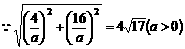
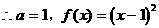 …………………4分
…………………4分
(2)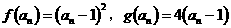
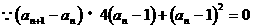
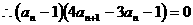
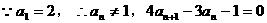 …………6分
…………6分
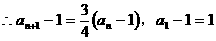 数列
数列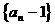 是首项为1,公比为
是首项为1,公比为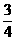 的等比数列…………8分
的等比数列…………8分
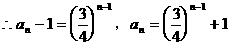 …………9分
…………9分
(3)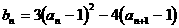
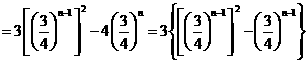 令
令 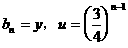 …………10分
…………10分
则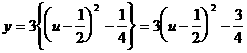
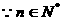 ,
,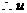 的值分别为
的值分别为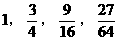 ……,经比较
……,经比较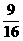 距
距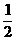 最近…………12分
最近…………12分
∴当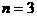 时,
时,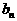 有最小值是
有最小值是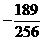 ,
………………………………13分
,
………………………………13分
当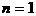 时,
时,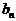 有最大值是0。
…………………………………14分
有最大值是0。
…………………………………14分
19、(本小题满分14分)已知函数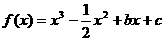
(1)若f(x)的图象有与x轴平行的直线,求b的取值范围;
(2)若f(x)在x=1处取得极值,且x∈(-1,2),f(x)<c2恒成立,求c的取值范围。
解:(1)f(x)=x3+ax2+bx+c,f¢(x)=3x2-x+b
由f¢(x)=0有实数解,所以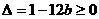
故b≤1/12
(2)x=1 f¢(x)=0的一根,可求得x=-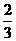 是另一根,f(x)=
是另一根,f(x)=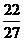 +c
+c
为极大值,而f(2)=2+c,则f(2)=2+c为最大值。
要使f(x)<c2(xÎ(-1,2))恒成立,只需c2≥f(2)=2+c
解得c≤-1或c≥2
18、(本题满分14分)
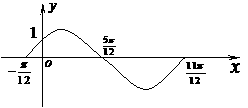
函数f1(x)=A sin (w x+ j ) (A>0, w >0, | j |< )的一段图象过点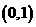 ,如图所示.
,如图所示.
(1)求函数f1 (x)的解析式;
 (2)将函数y= f1 (x)的图象按向量a = ( , 0)平移,得到函数 y =
f2 (x),求y=
f1 (x)+ f2 (x)的最大值,并求此时自变量
(2)将函数y= f1 (x)的图象按向量a = ( , 0)平移,得到函数 y =
f2 (x),求y=
f1 (x)+ f2 (x)的最大值,并求此时自变量 的集合.
的集合.
解:⑴ 由图知: T = ―(―) = p,于是 w = = 2 2分
设f1(x)=A sin (2x+j )
将函数f (x)=A sin 2x的图象向左平移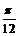 ,得f1(x)=A
sin (2x+j )的图象,
则
,得f1(x)=A
sin (2x+j )的图象,
则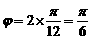 ,∴ f1(x)=A sin (2x+ ), 4分
,∴ f1(x)=A sin (2x+ ), 4分
将(0,1)代入f1(x)=A sin (2x+ ), 易得A=2 7分
故 f1(x) = 2 sin (2x+ ) 8分
⑵ 依题意: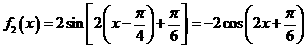 10分
10分
∴ 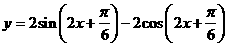
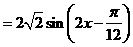 12分
12分
当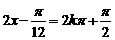 ,即
,即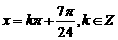 时,
时,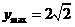
此时,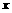 的取值集合为
的取值集合为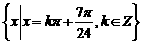 14分
14分
17、(本小题满分14分)
在等差数列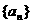 中,首项
中,首项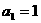 ,数列
,数列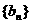 满足
满足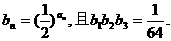
(1)求数列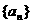 的通项公式;
的通项公式;
(2)求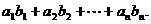
解(1)设等差数列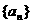 的公差为d,
的公差为d, 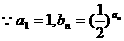 ,
,
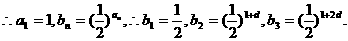
由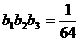 ,解得d=1.
5分
,解得d=1.
5分
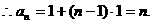 7分
7分
(2)由(1)得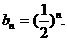
设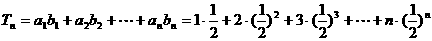 ,
,
则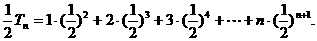 9分
9分
两式相减得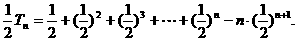 11分
11分
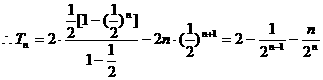 14分
14分
16、(本小题满分12分)
设f(x)=x3-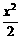 -2x+5.
-2x+5.
(1)求f(x)的单调区间;
(2)当x∈[1,2]时,f(x)<m恒成立,求实数m的取值范围.
解:(1)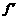 (x)=3x2-x-2=0,得x=1,-
(x)=3x2-x-2=0,得x=1,-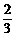 .在(-∞,-
.在(-∞,-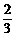 )和[1,+∞]上
)和[1,+∞]上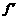 (x)>0,f(x)为增函数;在[-
(x)>0,f(x)为增函数;在[-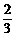 ,1]上
,1]上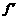 (x)<0,f(x)为减函数.所以所求f(x)的单调增区间为(-∞,-
(x)<0,f(x)为减函数.所以所求f(x)的单调增区间为(-∞,-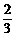 )和[1,+∞],单调减区间为[-
)和[1,+∞],单调减区间为[-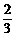 ,1]. 6分
,1]. 6分
(2)当x∈[1,2]时,显然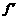 (x)>0,f(x)为增函数,f(x)≤f(2)=7.
(x)>0,f(x)为增函数,f(x)≤f(2)=7.
∴m>7. 12分
15、(本小题满分12分)
已知sin(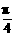 -x)=
-x)=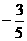 ,
, 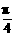 <x<
<x<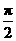 ,求
,求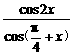 的值.
的值.
解:∵(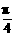 -x)+(
-x)+(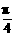 +x)=
+x)=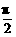 ,
,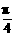 <x<
<x<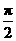
∴cos(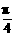 +x)=sin(
+x)=sin(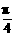 -x). cos(
-x). cos(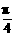 -x)=
-x)=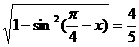 4分
4分
又cos2x=sin(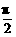 -2x)
-2x)
=sin2(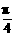 -x)=2sin(
-x)=2sin(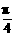 -x)cos(
-x)cos(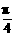 -x),
-x),
∴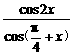 =2cos(
=2cos(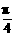 -x)=2×
-x)=2×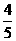 =
=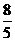 12分
12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com