
题目列表(包括答案和解析)
6. 函数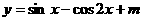 ,
,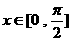 的最大值是
的最大值是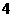 ,则函数的值域是( )。
,则函数的值域是( )。
A.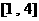 B.
B. 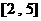 C.
C. 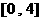 D.
D. 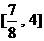
5. 如果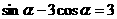 ,那么
,那么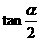 的值是( )。
的值是( )。
A. 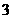 或不存在 B.
或不存在 B. 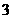 或
或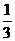 C.
C. 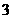 D.
D. 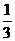
4. 使函数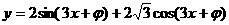 为奇函数,且在
为奇函数,且在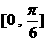 上是减函数的一个值是( )。
上是减函数的一个值是( )。
A. 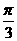 B.
B. 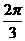 C.
C. 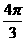 D.
D. 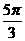
3. 若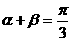 ,且
,且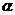 、
、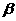 满足关系式
满足关系式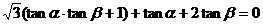 ,则
,则 ( )。
( )。
A. 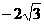 B.
B.  C.
C. 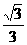 D.
D. 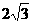
2. 已知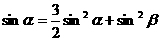 ,则函数
,则函数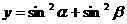 的值域是( )。
的值域是( )。
A. 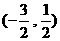 B.
B. 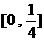 C.
C. 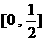 D.
D. 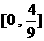
1. 函数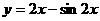 在
在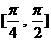 上的最小值是( )。
上的最小值是( )。
A. 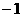 B.
B. 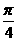 C.
C. 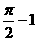 D.
D. 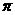
三角、向量综合复习训练
[模拟试题]
数学应用题的求解不同于一般的数学运算题,有人比喻它是数学中的小作文,因此解数学应用题要做到“有头有尾”,把问题中的普通语言转化为数学语言,引入变量与字母,画出图形,将数学建模的过程详细地写出来,建立数学模型后,要准确地求解,并注意计量单位的一致,最后对于所得数据不仅要思考或检验是否与实际吻合,而且要给出完整的答案。
3. 图像分析法。即通过对图像中的数量关系进行分析来建立问题数学模型的方法。
例3. (西红柿种植与销售问题)某蔬菜基地种植西红柿,由历年市场行情得知,从二月一日起的300天内,西红柿市场售价与上市时间的关系用图1的一条折线表示;西红柿的种植成本与上市时间的关系用图2的抛物线段表示,(1)写出图1表示的市场售价与时间的函数关系式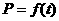 ;
;

写出图2表示的种植成本与时间的函数关系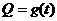 ;
;

(2)认定市场售价减去种植成本为纯收益,问何时上市的西红柿纯收益最大?(注:市场售价和种植成本的单位:元/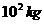 ,时间单位:天)
,时间单位:天)
读懂题目:(1)观察图像求出市场售价函数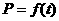 和种植成本函数
和种植成本函数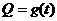 ;(2)由“市场售价减去种植成本为纯收益”建立纯收益函数
;(2)由“市场售价减去种植成本为纯收益”建立纯收益函数
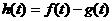
解题思路:(1)由图1可得市场售价与时间的函数关系为
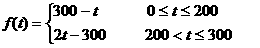
由图2可得种植成本与时间的函数关系为
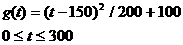
(2)解略。
2. 列表分析法。即通过列表的方式探索问题的数学模型的方法。
例2. (旅游业的投入产出问题)从社会效益和经济效益出发,某地投入资金进行生态环境建设,并以此发展旅游产业,根据规划,本年度投入800万元,以后每年投入将比上年减少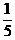 ,本年度当地旅游业收入估计为400万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加
,本年度当地旅游业收入估计为400万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加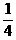 。(1)设
。(1)设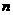 年内(本年度为第一年)总投入为
年内(本年度为第一年)总投入为 万元,旅游业总收入为
万元,旅游业总收入为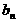 万元,写出它们的表达式;
万元,写出它们的表达式;
(2)至少经过几年旅游业的总收入才能超过总投入?
读懂题目:在研究旅游业的投入产出问题时,根据“本年度投入800万元,以后每年投入将比上年减少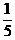 ”和“旅游业收入每年会比上年增加
”和“旅游业收入每年会比上年增加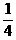 ”,其投入资金数列和收入(产出)数列均为等比数列,注意题目“设
”,其投入资金数列和收入(产出)数列均为等比数列,注意题目“设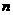 年内(本年度为第一年)总投入为
年内(本年度为第一年)总投入为 万元,旅游业总收入为
万元,旅游业总收入为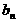 万元”中的“
万元”中的“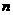 年内”说明“
年内”说明“ ”、“
”、“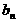 ”表示等比数列的前
”表示等比数列的前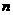 项和。
项和。
建立数学模型:(1)第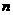 年的投入与收入资金数列列表如下
年的投入与收入资金数列列表如下
第几年 投入资金(万元) 旅游收入(万元)
|
1 |
800 |
400 |
|
2 |
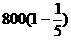 |
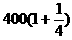 |
|
3 |
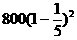 |
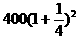 |
|
4 |
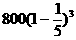 |
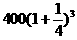 |
|
5 |
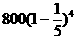 |
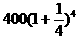 |
|
…… |
|
|
|
n |
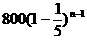 |
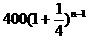 |
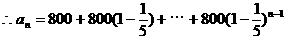 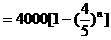 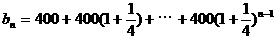 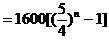 |
(2)略
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com