
题目列表(包括答案和解析)
(1)C (2)B (3) D (4)D(5) C (6) A(7)C (8)A (9)C (10)B (11)A (12)D
 (17)(本小题满分12分)
(17)(本小题满分12分)
已知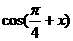 =
=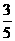 ,求
,求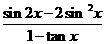 的值.
的值.
 (18)(本小题满分12分)
(18)(本小题满分12分)
已知等比数列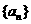 的公比为
的公比为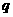 ,前n项的和为
,前n项的和为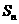 ,且
,且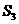 ,
,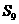 ,
,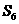 成等差数列.
成等差数列.
(Ⅰ)求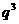 的值;
的值;
(Ⅱ)求证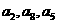 成等差数列.
成等差数列.
 (19) (本小题满分12分)
(19) (本小题满分12分)
一个口袋中装有大小相同的2个白球和3个黑球.
(Ⅰ)从中摸出两个球,求两球恰好颜色不同的概率;
(Ⅱ)从中摸出一个球,放回后再摸出一个球,求两球恰好颜色不同的概率.
注意:考生在(20甲)、(20乙)两题中选一题作答.如果两题都答,只以(20甲)计分.
 (20) (本小题满分12分)
(20) (本小题满分12分)
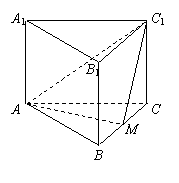 (甲)如图,正三棱柱
(甲)如图,正三棱柱 的底面边长为
的底面边长为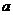 ,点
,点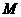 在边
在边 上,
上,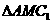 是以点M为直角顶点的等腰直角三角形.
是以点M为直角顶点的等腰直角三角形.
(Ⅰ) 求证点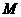 为边
为边 的中点;
的中点;
(Ⅱ) 求点 到平面
到平面 的距离;
的距离;
(Ⅲ) 求二面角 的大小.
的大小.
 (乙) 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=
(乙) 如图,直三棱柱ABC-A1B1C1中,底面是以∠ABC为直角的等腰直角三角形,AC=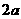 ,BB1=
,BB1=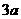 ,D为A1C1的中点,E为B1C的中点,
,D为A1C1的中点,E为B1C的中点,
(Ⅰ)求直线BE与A1C所成的角;
(Ⅱ)在线段AA1上是否存在点F,使CF⊥平面B1DF,若存在,求出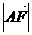 ;若不存在,说明理由.
;若不存在,说明理由.

(21)(本小题满分12分)
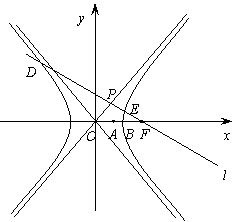 已知双曲线
已知双曲线 :
: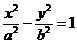
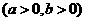 ,
, 是右顶点,
是右顶点,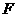 是右焦点, 点
是右焦点, 点 在
在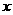 轴正半轴上,且满足
轴正半轴上,且满足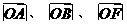 成等比数列,过
成等比数列,过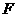 作双曲线
作双曲线 在第一、三象限的渐近线的垂线
在第一、三象限的渐近线的垂线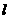 ,垂足为
,垂足为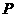 .
.
(Ⅰ)求证: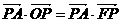 ;
;
(Ⅱ)若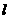 与双曲线
与双曲线 的左、右两支分别相交于点
的左、右两支分别相交于点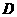 、
、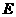 ,求双曲线
,求双曲线 的离心率
的离心率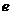 的取值范围.
的取值范围.
 (22)(本小题满分14分)
(22)(本小题满分14分)
设函数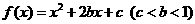 ,
,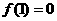 ,且方程
,且方程 +1=0有实根.
+1=0有实根.
(Ⅰ)证明: ;
;
(Ⅱ)证明: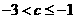 ;
;
(Ⅲ)若 是方程
是方程 +1=0的一个实根,判断
+1=0的一个实根,判断 的正负并加以证明.
的正负并加以证明.
高考数学模拟试卷2参考解答及评分标准
说明:
(13)若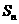 是数列
是数列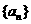 的前
的前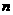 项的和,
项的和,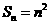 ,则
,则 .
.
(14) 若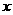 、
、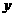 满足
满足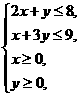 则
则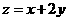 的最大值为
.
的最大值为
.
(15) 有 、
、 、
、 、
、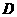 、
、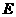 五名学生参加网页设计竞赛,决出了第一到第五的名次,
五名学生参加网页设计竞赛,决出了第一到第五的名次, 、
、 两位同学去问成绩,老师对
两位同学去问成绩,老师对 说:“你没能得第一名”.又对
说:“你没能得第一名”.又对 说:“你是第三名”,从这个问题分析,这五人的名次排列共有
种可能(用数字作答).
说:“你是第三名”,从这个问题分析,这五人的名次排列共有
种可能(用数字作答).
(16) 若对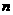 个向量
个向量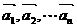 存在
存在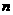 个不全为零的实数
个不全为零的实数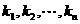 ,使得
,使得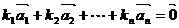 成立,则称向量
成立,则称向量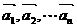 为“线性相关”.依此规定,
能说明
为“线性相关”.依此规定,
能说明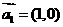 ,
,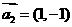 ,
,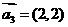 “线性相关”的实数
“线性相关”的实数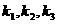 依次可以
依次可以
取 (写出一组数值即可,不必考虑所有情况).
四个选项中,有且只有一项是符合题目要求的.
(1) 设M和m分别表示函数 的最大值和最小值,则M+m等于
的最大值和最小值,则M+m等于
(A)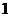 (B)
(B)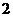 (C)
(C)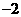 (D)-1
(D)-1
(2) 设集合M=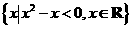 ,N=
,N=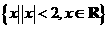 ,则
,则
(A)N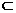 M (B)M
M (B)M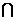 N=M (C)M
N=M (C)M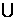 N=M (D)M
N=M (D)M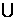 N=
N=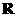
(3) 若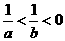 ,则下列结论不正确的是
,则下列结论不正确的是
(A)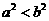 (B)
(B)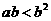 (C)
(C)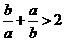 (D)
(D)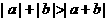
(4) 直线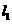 ,
,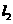 互相平行的一个充分条件是
互相平行的一个充分条件是
(A) 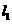 ,
,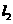 都平行于同一个平面
(B)
都平行于同一个平面
(B) 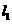 ,
,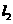 与同一个平面所成的角相等
与同一个平面所成的角相等
(C) 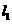 平行于
平行于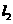 所在的平面
(D)
所在的平面
(D) 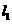 ,
,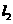 都垂直于同一个平面
都垂直于同一个平面
(5) 若二项式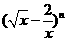 的展开式的第5项是常数项,则自然数
的展开式的第5项是常数项,则自然数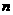 的值为
的值为
(A)6 (B)10 (C)12 (D)15
(6) 已知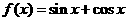 ,则
,则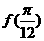 的值为
的值为
(A) 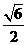 (B)
(B)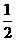 (C)
(C)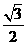 (D)
(D) 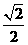
(7) 函数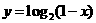 的图象是
的图象是
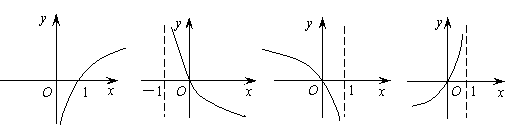 (A)
(B) (C)
(D)
(A)
(B) (C)
(D)
(8)椭圆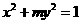 的焦点在
的焦点在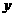 轴上,长轴长是短轴长的两倍,则
轴上,长轴长是短轴长的两倍,则 的值为
的值为
(A)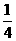 (B)
(B)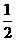 (C)2
(D)4
(C)2
(D)4
(9) 若曲线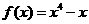 在点P处的切线平行于直线
在点P处的切线平行于直线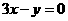 ,则点P的坐标为
,则点P的坐标为
(A)(1,3) (B)(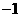 ,3) (C)(1,0) (D)(-1,0)
,3) (C)(1,0) (D)(-1,0)
(10) 已知函数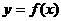 是R上的偶函数,且在
是R上的偶函数,且在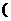
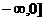 上是减函数,若
上是减函数,若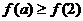 ,则实数a的取值范围是
,则实数a的取值范围是
(A)a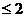 (B) a
(B) a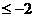 或a
或a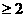 (C) a
(C) a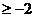 (D)
(D)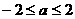
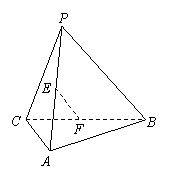 (11)如图,E、F分别是三棱锥
(11)如图,E、F分别是三棱锥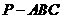 的棱AP、BC的中点,
的棱AP、BC的中点, 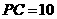 ,
,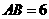 ,EF=7,则异面直线AB与PC所成的角为
,EF=7,则异面直线AB与PC所成的角为
(A) 600 (B)450 (C) 300 (D)1200
(12) 圆心在抛物线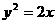 (
(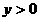 )上,并且与抛物线
)上,并且与抛物线
的准线及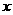 轴都相切的圆的方程是
轴都相切的圆的方程是
(A)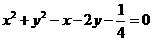 (B)
(B)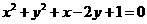
(C)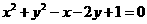 (D)
(D)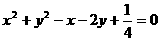
第Ⅱ卷(非选择题共90分)

22.(本题满分14分) 已知函数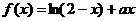 在开区间(0,1)内是增函数.
在开区间(0,1)内是增函数.
(Ⅰ) 求实数a的取值范围;
(Ⅱ) 若数列{an}满足a1∈(0,1),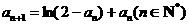 ,证明:
,证明: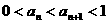 .
.
(Ⅲ) 若数列{bn}满足b1∈(0,1),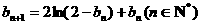 ,问数列{bn}是否单调?
,问数列{bn}是否单调?
(Ⅰ) 解: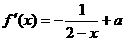 ,由于f (x)在(0,1)内是增函数,
,由于f (x)在(0,1)内是增函数,
∴ 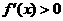 ,即
,即 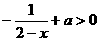 在x∈(0,1)时恒成立.
在x∈(0,1)时恒成立.
∴ 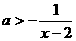 恒成立,
恒成立,
而 -2<x-2<-1,
∴ 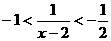 ,
,
即 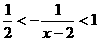 ,
,
∴ a≥1即为所求.
(Ⅱ) 证明:由题设知,当n=1时,a1∈(0,1).
假设当n=k时,有ak∈(0,1),则
当n=k+1时,有 且
且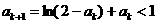 (由第一问知f(x)=ln(2-x)+x在(0,1)上是增函数),
(由第一问知f(x)=ln(2-x)+x在(0,1)上是增函数),
∴ n=k+1时命题成立,故0<an<1,n∈N*.
又 ∵ 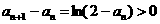 ,
,
∴ 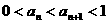 .
.
(Ⅲ) 数列{bn}不具有单调性.
令 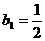 , 则
, 则 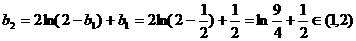 ,
,
∴ b2>b1.
又 ∵ 1<b2<2,0<2-b2<1,
∴ ln(2-b2)<0,
∴ 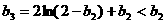 .
.
由此表明数列{bn}没有单调性.
21.(本题满分12分) 某保险公司新开设了一项保险业务,若在一年内事件E发生,该公司要赔偿a元.设在一年内E发生的概率为p,为使公司收益的期望值等于a的百分之十,公司应要求顾客交多少保险金?
解:设保险公司要求顾客交x元保险金,若以x表示公司每年的收益额,则x是一个随机变量,其分布列为:
|
x |
x |
x-a |
|
P |
1-p |
p |
因此,公司每年收益的期望值为
Ex=x(1-p)+(x-a)·p=x-ap.
为使公司收益的期望值等于a的百分之十,
只需Ex=0.1a,即x-ap=0.1a,
故可得x=(0.1+p)a.
即顾客交的保险金为(0.1+p)a时,可使公司期望获益10%a.
说明:当事件E发生的概率较小时,即使赔偿数目较大,保险公司仍可获益.例如当P=0.001,a=10000元时,根据上述赔偿办法,顾客只需交纳(0.1+0.001)×10000=1010元保险金,但保险公司仍可期望获益10%a=1000元,当保险公司的顾客较多时,其效益十分可观.
20.(本题满分12分) 已知f(x)是定义在(-∞,0)∪(0,+∞)上的奇函数,当x<0时,f(x)=x2-x-2,解不等式f(x)>0.
解: 设x>0,则 -x<0.
∴ f (-x)=(-x)2-(-x)-2=x2+x-2.
而f (x) 是奇函数,
∴ f (-x)=-f (x),
于是 f (x)=-x2-x+2,x>0.
∴ 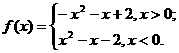
(1) 由 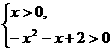 得
得 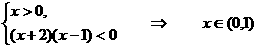 .
.
(2) 由 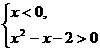 得
得 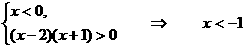 .
.
综上所述,不等式f (x)>0的解集为{x∣x<-1或0<x<1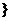 .
.
19.(本题满分12分) 已知p:∣1-2x∣≤ 5,q:x2-4x+4-9m2 ≤ 0 (m>0),若 p是
p是 q的充分而不必要条件,求实数m的取值范围.
q的充分而不必要条件,求实数m的取值范围.
解:解不等式可求得:
p:-2≤x≤3, q:2-3m≤x≤2+3m (m>0).
则  p:A={x∣x<-2或x>3},
p:A={x∣x<-2或x>3},
 q:B={x∣x<2-3m或x>2+3m,m>0
q:B={x∣x<2-3m或x>2+3m,m>0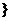 .
.
由已知  p
p 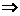
 q,得A
q,得A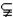 B,从而
B,从而
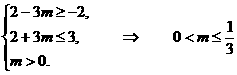 .
.
(上述不等式组中等号不能同时取).
经验证 为所求实数m的取值范围.
为所求实数m的取值范围.
18.(本题满分12分) 已知函数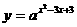 在[0,2]上有最小值8,求正数a的值.
在[0,2]上有最小值8,求正数a的值.
解:设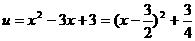 ,
,
当x∈[0,2]时,可得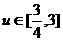 .
.
(1) 若a>1时,则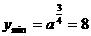 ,解得a=16>1.
,解得a=16>1.
(2) 若0<a<1时,则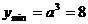 ,解得a=2,此与0<a<1矛盾,舍去.
,解得a=2,此与0<a<1矛盾,舍去.
故正数a =16.
17.解: (Ⅰ) 由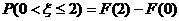 =
=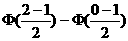
=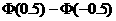 =2
=2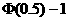
=2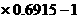 =0.3830.
=0.3830.
(Ⅱ) 由已知可得 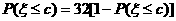 ,
,
∴ 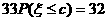 ,
,
即 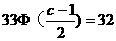 ,
,
∴ 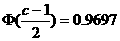 ,
,
∴ 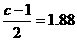 , c=4.76.
, c=4.76.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com