
题目列表(包括答案和解析)
1.在 中,
中,
 四个条件中,是
四个条件中,是 的充分且必要条件的有:( )
的充分且必要条件的有:( )
(A)1个; (B)2个; (C)3个 ; (D)4个.
22、解:(1)由f(x)=-(cosx-a)2+a3+a2-a+1
令t=cosx,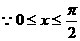 ,
0≤t≤1
,
0≤t≤1
则g(t)=-(t-a)2+a3+a2-a+1
10若a<0,则当t=0时,M(a)=g(0)=a3-a+1
20若0≤a≤1,则当t=a时,M(a)=g(a)=a3+a2-a+1
30若a>1,则当t=1时,M(a)=g(1)=a3+a
∴M(a)=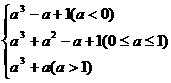
(2)当-1≤a<0时,M(a)=a3-a+1
∴M’(a)=3a2-1=3(a+ )(a-
)(a- )
)
令M’(a)=0,得a1=- ,或a2=
,或a2= (舍去)
(舍去)
且M(- )=(-
)=(- )3-(-
)3-(- )+1=
)+1= +1
+1
当0≤a<1时,M(a)=a3+a2-a+1
∴M’(a)=3a2+2a-1=(3a-1)(a+1)
令M’(a)=0,得a3= ,或a4=-1(舍去)
,或a4=-1(舍去)
且M( )=(
)=( )3+(
)3+( )2-
)2- +1=
+1=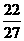
列表如下
|
a |
-1 |
(1,- ) ) |
- |
(- ,0) ,0) |
0 |
(0, ) ) |
 |
( ,1) ,1) |
1 |
|
M’(a) |
|
+ |
|
|
|
- |
|
+ |
|
|
M(a) |
1 |
|
 +1 +1 |
|
1 |
|
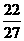 |
|
2 |
从上表可知:
当a=1时,M(a)取得最大值2
当a= 时,M(a)取得最小值
时,M(a)取得最小值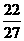 。
。
21、 (1)由
(1)由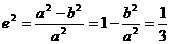 ,得
,得
∵直线 :y=x+2与圆x2+y2=b2相切,∴
:y=x+2与圆x2+y2=b2相切,∴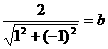 ,解得
,解得 ,则a2=3。
,则a2=3。
故所求椭圆C1的方程为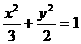 。
。
(2)椭圆C1的左焦点为F(-1,0),左准线为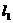 :x=-3。
:x=-3。
如图,连结MF,则|MF|=|MP|,∴点M的轨迹C2是以F为焦点,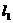 为准线的抛物线,其方程为y2=4(x+2),故Q(-2,0)。设
为准线的抛物线,其方程为y2=4(x+2),故Q(-2,0)。设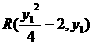 、
、 ,由QR⊥RS得
,由QR⊥RS得

化简得y2=-(y1+ )
)
∴y22=y12+ ≥2×16+32=64
≥2×16+32=64
∵|QS|2=[( -2)+2]2+y22=
-2)+2]2+y22=
∴当y22=64时,|QS|min= .
.
故|QS|的取值范围是[8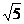 ,+∞)。
,+∞)。
20、 (1)函数y=f(t)的定义域为[0,+∞);值域为{y|y=2n,n∈N*}
 (2)
(2)
(3)y=
19、(1) ∵PA⊥底面ABC,∴PA⊥BE
又∵△ABC是正三角形,且E为AC的中点,∴BE⊥CA
又PA ,∴BE⊥平面PAC
,∴BE⊥平面PAC
∵BE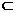 平面PBE,∴平面PBE⊥平面PAC。
平面PBE,∴平面PBE⊥平面PAC。
(2)取CD的中点F,则点F即为所求。
∵E、F分别为CA、CD的中点,∴EF//AD
又EF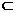 平面PEF,AD
平面PEF,AD 平面PEF,∴AD//平面PEF。
平面PEF,∴AD//平面PEF。
(3)
18、(1)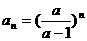 (2)
(2)
17、①当m≠ 时,A、B、C三点能构成三角形;
时,A、B、C三点能构成三角形;
②当m= 时,三角形ABC为直角三角形,且∠A=90°。
时,三角形ABC为直角三角形,且∠A=90°。
13、( ,0) 14、
,0) 14、 15、10
16、1
15、10
16、1
1、A 2、D 3、A 4、A 5、C 6、A 7、B 8、C 9、A 10、C 11、B 12、C
22、设函数f(x)=sin2x+2a·cosx+a3-a(0≤x≤ )
)
(1)求f(x)的最大值M(a)。
(2)当a∈[-1,1]时,求函数M(a)的最值。
[答案]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com